8  Das Typsystem von Julia

Man kann umfangreiche Programme in Julia schreiben, ohne auch nur eine einzige Typdeklaration verwenden zu müssen. Das ist natürlich Absicht und soll die Arbeit der Anwender vereinfachen.

Wir blicken jetzt trotzdem mal unter die Motorhaube.

8.1 Die Typhierarchie am Beispiel der numerischen Typen

Das Typsystem hat die Struktur eines Baums, dessen Wurzel der Typ Any ist. Mit den Funktionen subtypes() und supertype() kann man den Baum erforschen. Sie zeigen alle Kinder bzw. die Mutter eines Knotens an.

subtypes(Int64)
Type[]

Das Ergebnis ist eine leere Liste von Typen. Int64 ist ein sogenannter konkreter Typ und hat keine Untertypen.

Wir klettern jetzt mal die Typhierarchie auf diesem Ast nach oben bis zur Wurzel (Informatiker-Bäume stehen bekanntlich immer auf dem Kopf).

supertype(Int64)
Signed
supertype(Signed)
Integer
supertype(Integer)
Real
supertype(Real)
Number
supertype(Number)
Any

Das wäre übrigens auch schneller gegangen: Die Funktion supertypes() (mit Plural-s) zeigt alle Vorfahren an.

supertypes(Int64)
(Int64, Signed, Integer, Real, Number, Any)

Nun kann man sich die Knoten angucken:

subtypes(Real)
4-element Vector{Any}:
 AbstractFloat
 AbstractIrrational
 Integer
 Rational

Mit einer kleinen rekursiven Funktion kann man schnell einen ganzen (Unter-)Baum ausdrucken:

function show_subtype_tree(T, i=0)
    println("       "^i, T)
    for Ts ∈ subtypes(T)
        show_subtype_tree(Ts, i+1)
    end
end

show_subtype_tree(Number)
Number
       Complex
       Real
              AbstractFloat
                     BigFloat
                     Float16
                     Float32
                     Float64
              AbstractIrrational
                     Irrational
              Integer
                     Bool
                     Signed
                            BigInt
                            Int128
                            Int16
                            Int32
                            Int64
                            Int8
                     Unsigned
                            UInt128
                            UInt16
                            UInt32
                            UInt64
                            UInt8
              Rational

Hier das Ganze nochmal als Bild (gemacht mit LaTeX/TikZ)

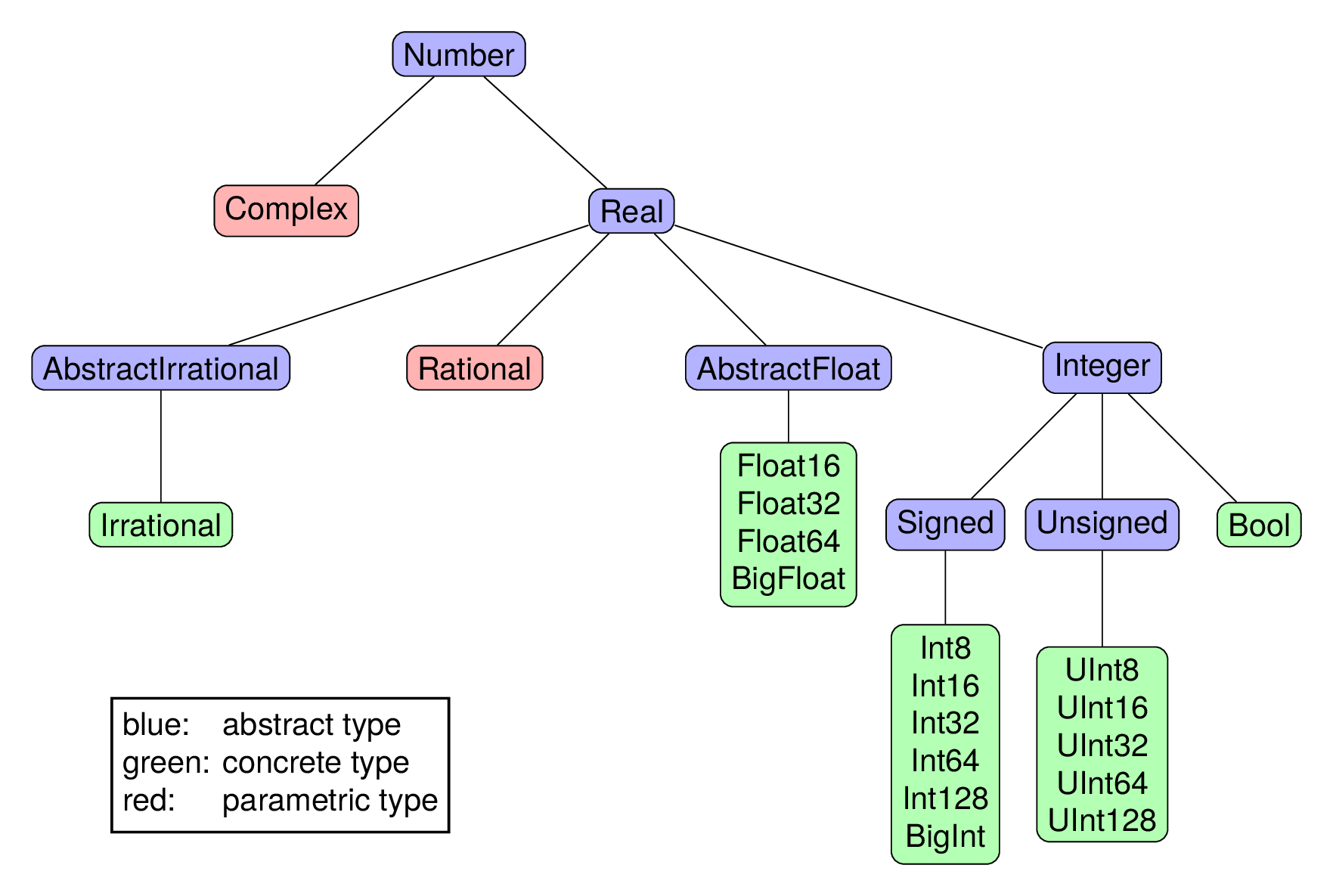
Natürlich hat Julia nicht nur numerische Typen. Die Anzahl der direkten Abkömmlinge (Kinder) von Any ist

length(subtypes(Any))
625

und mit (fast) jedem Paket, das man mit using ... lädt, werden es mehr.

8.2 Abstrakte und Konkrete Typen

  • Ein Objekt hat immer einen konkreten Typ.
  • Konkrete Typen haben keine Untertypen mehr, sie sind immer „Blätter“ des Baumes.
  • Konkrete Typen spezifizieren eine konkrete Datenstruktur.
  • Abstrakte Typen können nicht instanziiert werden, d.h., es gibt keine Objekte mit diesem Typ.
  • Sie definieren eine Menge von konkreten Typen und gemeinsame Methoden für diese Typen.
  • Sie können daher in der Definition von Funktionstypen, Argumenttypen, Elementtypen von zusammengesetzten Typen u.ä. verwendet werden.

Zum Deklarieren und Testen der “Abstammung” innerhalb der Typhierarchie gibt es einen eigenen Operator:

Int64 <: Number
true

Zum Testen, ob ein Objekt einen bestimmten Typ (oder einen abstrakten Supertyp davon) hat, dient isa(object, typ). Es wird meist in der Infix-Form verwendet und sollte als Frage x is a T? gelesen werden.

x = 17.2

42 isa Int64,  42 isa Real,  x isa Real,   x isa Float64,   x isa Integer
(true, true, true, true, false)

Da abstrakte Typen keine Datenstrukturen definieren, ist ihre Definition recht schlicht. Entweder sie stammen direkt von Any ab:

abstract type MySuperType end

supertype(MySuperType)
Any

oder von einem anderen abstrakten Typ:

abstract type MySpecialNumber <: Integer end

supertypes(MySpecialNumber)
(MySpecialNumber, Integer, Real, Number, Any)

Mit der Definition werden die abstrakten Typen an einer Stelle des Typ-Baums “eingehängt”.

8.3 Die numerischen Typen Bool und Irrational

Da sie im Baum der numerischen Typen zu sehen sind, seien sie kurz erklärt:

Bool ist numerisch im Sinne von true=1, false=0:

true + true + true, false - true, sqrt(true), true/4
(3, -1, 1.0, 0.25)

Irrational ist der Typ einiger vordefinierter Konstanten wie π und ℯ. Laut Dokumentation ist Irrational ein “Number type representing an exact irrational value, which is automatically rounded to the correct precision in arithmetic operations with other numeric quantities”.

8.4 Union-Typen

Falls die Baum-Hierarchie nicht ausreicht, kann man auch abstrakte Typen als Vereinigung beliebiger (abstrakter und konkreter) Typen definieren.

IntOrString = Union{Int64,String}
Union{Int64, String}
Beispiel

Das Kommando methods(<) zeigt, dass unter den über 70 Methoden, die für den Vergleichsoperator definiert sind, einige auch union types verwenden, z.B. ist

 <(x::Union{Float16, Float32, Float64}, y::BigFloat)

eine Methode für den Vergleich einer Maschinenzahl fester Länge mit einer Maschinenzahl beliebiger Länge.

8.5 Zusammengesetzte (composite) Typen: struct

Eine struct ist eine Zusammenstellung von mehreren benannten Feldern und definiert einen konkreten Typ.

abstract type Point end

mutable struct Point2D <: Point
    x :: Float64
    y :: Float64
end

mutable struct Point3D <: Point
    x :: Float64
    y :: Float64
    z :: Float64
end

Wie wir schon bei Ausdrücken der Form x = Int8(33) gesehen haben, kann man Typnamen direkt als Konstruktoren einsetzen:

p1 = Point2D(1.4, 3.5)
Point2D(1.4, 3.5)
p1 isa Point3D,  p1 isa Point2D,   p1 isa Point
(false, true, true)

Die Felder einer struct können über ihren Namen mit dem .-Operator adressiert werden.

p1.y
3.5

Da wir unsere struct als mutable deklariert haben, können wir das Objekt p1 modifizieren, indem wir den Feldern neue Werte zuweisen.

p1.x = 3333.4
p1
Point2D(3333.4, 3.5)

Informationen über den Aufbau eines Typs oder eines Objekts von diesem Typ liefert dump().

dump(Point3D)
Point3D <: Point
  x::Float64
  y::Float64
  z::Float64
 dump(p1)
Point2D
  x: Float64 3333.4
  y: Float64 3.5

8.6 Funktionen und Multiple dispatch

Objekte, Funktionen, Methoden

In klassischen objektorientierten Sprachen wie C++/Java haben Objekte üblicherweise mit ihnen assoziierte Funktionen, die Methoden des Objekts.

In Julia gehören Methoden zu einer Funktion und nicht zu einem Objekt. (Eine Ausnahme sind die Konstruktoren, also Funktionen, die genauso heißen wie ein Typ und ein Objekt dieses Typs erzeugen.)

Sobald man einen neuen Typ definiert hat, kann man sowohl neue als auch bestehende Funktionen um neue Methoden für diesen Typ ergänzen.

  • Eine Funktion kann mehrfach für verschiedene Argumentlisten (Typ und Anzahl) definiert werden.
  • Die Funktion hat dann mehrere Methoden.
  • Beim Aufruf wird an Hand der konkreten Argumente entschieden, welche Methode genutzt wird (multiple dispatch).
  • Es ist typisch für Julia, dass für Standardfunktionen viele Methoden definiert sind. Diese können problemlos um weitere Methoden für eigene Typen erweitert werden.

Den Abstand zwischen zwei Punkten implementieren wir als Funktion mit zwei Methoden:

function distance(p1::Point2D, p2::Point2D)
    sqrt((p1.x-p2.x)^2 + (p1.y-p2.y)^2)
end

function distance(p1::Point3D, p2::Point3D)
    sqrt((p1.x-p2.x)^2 + (p1.y-p2.y)^2 + (p1.z-p2.z)^2)
end
distance (generic function with 2 methods)
distance(p1, Point2D(2200, -300))
1173.3319266090054

Wie schon erwähnt, zeigt methods() die Methodentabelle einer Funktion an:

methods(distance)
# 2 methods for generic function distance from Main.Notebook:

Das Macro @which, angewendet auf einen vollen Funktionsaufruf mmit konkreter Argumentliste, zeigt an, welche Methode zu diesen konkreten Argumenten ausgewählt wird:

@which sqrt(3.3)
sqrt(x::Union{Float32, Float64}) in Base.Math at math.jl:607 
z = "Hallo" * '!'
println(z)

@which "Hallo" * '!'
Hallo!
*(s1::Union{AbstractChar, AbstractString}, ss::Union{AbstractChar, AbstractString}...) in Base at strings/basic.jl:261

Methoden können auch abstrakte Typen als Argument haben:

"""
  Berechnet den Winkel ϕ (in Grad) der Polarkoordinaten (2D) bzw.
    Kugelkoordinaten (3D) eines Punktes
"""
function phi_winkel(p::Point)
    atand(p.y, p.x)
end

phi_winkel(p1)
0.0601593431937626

Ein in triple quotes eingeschlossene Text unmittelbat vor der Funktionsdefinition wird automatisch in die Hilfe-Datenbank von Julia integriert:

?phi_winkel
search: phi_winkel

Berechnet den Winkel ϕ (in Grad) der Polarkoordinaten (2D) bzw. Kugelkoordinaten (3D) eines Punktes

Beim multiple dispatch wird die Methode angewendet, die unter allen passenden die spezifischste ist. Hier eine Funktion mit mehreren Methoden (alle bis auf die letzte in der kurzen assignment form geschrieben):

f(x::String, y::Number)  = "Args: String + Zahl"
f(x::String, y::Int64)   = "Args: String + Int64"
f(x::Number, y::Int64)   = "Args: Zahl   + Int64"
f(x::Int64,  y:: Number) = "Args: Int64  + Zahl"
f(x::Number)             = "Arg: eine Zahl"

function f(x::Number, y::Number, z::String) 
    return "Arg: 2 x Zahl + String"
end
f (generic function with 6 methods)

Hier passen die ersten beiden Methoden. Gewählt wird die zweite, da sie spezifischer ist, Int64 <: Number.

f("Hallo", 42)
"Args: String + Int64"

Es kann sein, dass diese Vorschrift zu keinem eindeutigen Ergebnis führt, wenn man seine Methoden schlecht gewählt hat.

f(42, 42)
MethodError: f(::Int64, ::Int64) is ambiguous.

Candidates:
  f(x::Int64, y::Number)
    @ Main.Notebook ~/Julia/23/Book-ansipatch/chapters/types.qmd:314
  f(x::Number, y::Int64)
    @ Main.Notebook ~/Julia/23/Book-ansipatch/chapters/types.qmd:313

Possible fix, define
  f(::Int64, ::Int64)

Stacktrace:
 [1] top-level scope
   @ ~/Julia/23/Book-ansipatch/chapters/types.qmd:328

8.7 Parametrisierte numerische Typen: Rational und Complex

  • Für rationale Zahlen (Brüche) verwendet Julia // als Infix-Konstruktor:
@show Rational(23, 17)    4//16 + 1//3;
Rational(23, 17) = 23//17
4 // 16 + 1 // 3 = 7//12
  • Die imaginäre Einheit \(\sqrt{-1}\) heißt im
@show Complex(0.4)     23 + 0.5im/(1-2im);
Complex(0.4) = 0.4 + 0.0im
23 + (0.5im) / (1 - 2im) = 22.8 + 0.1im

Rational und Complex bestehen, ähnlich wie unser Point2D, aus 2 Feldern: Zähler und Nenner bzw. Real- und Imaginärteil.

Der Typ dieser Felder ist allerdings nicht vollständig festgelegt. Rational und Complex sind parametrisierte Typen.

x = 2//7 
@show typeof(x);
typeof(x) = Rational{Int64}
y = BigInt(2)//7 
@show typeof(y)    y^48;
typeof(y) = Rational{BigInt}
y ^ 48 = 281474976710656//36703368217294125441230211032033660188801
x = 1 + 2im
typeof(x)
Complex{Int64}
y = 1.0 + 2.0im
typeof(y)
ComplexF64 (alias for Complex{Float64})

Die konkreten Typen Rational{Int64}, Rational{BigInt},…, Complex{Int64}, Complex{Float64}}, … sind Subtypen von Rational bzw. Complex.

Rational{BigInt} <: Rational
true

Die Definitionen sehen etwa so aus:

struct MyComplex{T<:Real} <: Number
    re::T
    im::T
end

struct MyRational{T<:Integer} <: Real
    num::T
    den::T
end

Die erste Definition besagt:

  • MyComplex hat zwei Felder re und im, beide vom gleichen Typ T.
  • Dieser Typ T muss ein Untertyp von Real sein.
  • MyComplex und alle seine Varianten wie MyComplex{Float64} sind Untertypen von Number.

und die zweite besagt analog:

  • MyRational hat zwei Felder num und den, beide vom gleichen Typ T.
  • Dieser Typ T muss ein Untertyp von Integer sein.
  • MyRational und seine Varianten sind Untertypen von Real.

Nun ist ℚ\(\subset\) ℝ, oder auf julianisch Rational <: Real. Also können die Komponenten einer komplexen Zahl auch rational sein:

z = 3//4 + 5im
dump(z)
Complex{Rational{Int64}}
  re: Rational{Int64}
    num: Int64 3
    den: Int64 4
  im: Rational{Int64}
    num: Int64 5
    den: Int64 1

Diese Strukturen sind ohne das mutable-Attribut definiert, also immutable:

x = 2.2 + 3.3im
println("Der Realteil ist: $(x.re)")

x.re = 4.4
Der Realteil ist: 2.2
setfield!: immutable struct of type Complex cannot be changed
Stacktrace:
 [1] setproperty!(x::ComplexF64, f::Symbol, v::Float64)
   @ Base ./Base.jl:53
 [2] top-level scope
   @ ~/Julia/23/Book-ansipatch/chapters/types.qmd:418

Das ist so üblich. Wir betrachten das Objekt 9 vom Typ Int64 ja auch als unveränderlich. Das Folgende geht natürlich trotzdem:

x += 2.2
4.4 + 3.3im

Hier wird ein neues Objekt vom Typ Complex{Float64} erzeugt und x zur Referenz auf dieses neue Objekt gemacht.

Die Möglichkeiten des Typsystems verleiten leicht zum Spielen. Hier definieren wir eine struct, die wahlweise eine Maschinenzahl oder ein Paar von Ganzzahlen enthalten kann:

struct MyParms{T <: Union{Float64, Tuple{Int64, Int64}}}
    param::T
end

p1 = MyParms(33.3)
p2 = MyParms( (2, 4) )

@show p1.param  p2.param;
p1.param = 33.3
p2.param = (2, 4)

8.8 Typen als Objekte

  1. Typen sind ebenfalls Objekte. Sie sind Objekte einer der drei “Meta-Typen”

    • Union (Union-Typen)
    • UnionAll (parametrisierte Typen)
    • DataType (alle konkreten und sonstige abstrakte Typen)
@show    23779 isa Int64       Int64 isa DataType;
23779 isa Int64 = true
Int64 isa DataType = true
@show  2im isa Complex         Complex isa UnionAll;
2im isa Complex = true
Complex isa UnionAll = true
@show  2im isa Complex{Int64}     Complex{Int64} isa DataType;
2im isa Complex{Int64} = true
Complex{Int64} isa DataType = true

Diese 3 konkreten “Meta-Typen” sind übrigens Subtypen des abstrakten “Meta-Typen” Type.

subtypes(Type)
4-element Vector{Any}:
 Core.TypeofBottom
 DataType
 Union
 UnionAll
  1. Damit können Typen auch einfach Variablen zugewiesen werden:
x3 = Float64
@show   x3(4)      x3 <: Real   x3==Float64  ;
x3(4) = 4.0
x3 <: Real = true
x3 == Float64 = true

Dies zeigt auch, dass die Style-Vorgaben in Julia wie „Typen und Typvariablen starten mit Großbuchstaben, sonstige Variablen und Funktionen werden klein geschrieben.“ nur Konventionen sind und von der Sprache nicht erzwungen werden.

Man sollte sie trotzdem einhalten, um den Code lesbar zu halten.

Wenn man solche Zuweisungen mit const für dauerhaft erklärt, entsteht ein
type alias.

const MyCmplxF64 = MyComplex{Float64}

z = MyCmplxF64(1.1, 2.2)
typeof(z)
MyComplex{Float64}
  1. Typen können Argumente von Funktionen sein.
function myf(x, S, T)
    if S <: T
        println("$S is subtype of $T")
    end
    return S(x)
end

z = myf(43, UInt16, Real)

@show z  typeof(z);
UInt16 is subtype of Real
z = 0x002b
typeof(z) = UInt16

Wenn man diese Funktion mit Typsignaturen definieren möchte, kann man natürlich

function myf(x, S::Type, T::Type) ... end

schreiben. Üblicher ist hier die (dazu äquivalente) spezielle Syntax

function myf(x, ::Type{S}, ::Type{T}) where {S,T} ... end

bei der man in der where-Klausel auch noch Einschränkungen an die zulässigen Werte der Typvariablen S und T stellen kann.

Wie definiere ich eine spezielle Methode von myf, die nur aufgerufen werden soll, wenn S und T gleich Int64 sind? Das ist folgendermaßen möglich:

function myf(x, ::Type{Int64}, ::Type{Int64}) ... end

Type{Int64} wirkt wie ein “Meta-Typ”, dessen einzige Instanz der Typ Int64 ist.

  1. Es gibt zahlreiche Operationen mit Typen als Argumenten. Wir haben schon <:(T1, T2), supertype(T), supertypes(T), subtypes(T) gesehen. Erwähnt seien noch typejoin(T1,T2) (nächster gemeinsamer Vorfahre im Typbaum) und Tests wie isconcretetype(T), isabstracttype(T), isstructtype(T).

8.9 Invarianz parametrisierter Typen

Kann man in parametrisierten Typen auch nicht-konkrete Typen einsetzen? Gibt es Complex{AbstractFloat} oder Complex{Union{Float32, Int16}}?

Ja, die gibt es; und es sind konkrete Typen, man kann also Objekte von diesem Typ erzeugen.

z5 = Complex{Integer}(2, 0x33)
dump(z5)
Complex{Integer}
  re: Int64 2
  im: UInt8 0x33

Das ist eine heterogene Struktur. Jede Komponente hat einen individuellen Typ T, für den T<:Integer gilt.

Nun gilt zwar

Int64 <: Integer
true

aber es gilt nicht, dass

Complex{Int64} <: Complex{Integer}
false

Diese Typen sind beide konkret. Damit können sie in der Typhierarchie von Julia nicht in einer Sub/Supertype-Relation zueinander stehen. Julias parametrisierte Typen sind in der Sprache der theoretischen Informatik invariant. (Wenn aus S<:T folgen würde, dass auch ParamType{S} <: ParamType{T} gilt, würde man von Kovarianz sprechen.)

8.10 Generische Funktionen

Der übliche (und in vielen Fällen empfohlene!) Programmierstil in Julia ist das Schreiben generischer Funktionen:

function fsinnfrei1(x, y)
    return x * x * y
end
fsinnfrei1 (generic function with 1 method)

Diese Funktion funktioniert sofort mit allen Typen, für die die verwendeten Operationen definiert sind.

fsinnfrei1( Complex(2,3), 10),  fsinnfrei1("Hallo", '!')
(-50 + 120im, "HalloHallo!")

Man kann natürlich Typ-Annotationen benutzen, um die Verwendbarkeit einzuschränken oder um unterschiedliche Methoden für unterschiedliche Typen zu implementieren:

function fsinnfrei2(x::Number, y::AbstractFloat)
    return x * x * y
end

function fsinnfrei2(x::String, y::String)
    println("Sorry, I don't take strings!")
end


@show fsinnfrei2(18, 2.0)   fsinnfrei2(18, 2);
fsinnfrei2(18, 2.0) = 648.0
MethodError: no method matching fsinnfrei2(::Int64, ::Int64)
The function `fsinnfrei2` exists, but no method is defined for this combination of argument types.

Closest candidates are:
  fsinnfrei2(::Number, ::AbstractFloat)
   @ Main.Notebook ~/Julia/23/Book-ansipatch/chapters/types.qmd:589
  fsinnfrei2(::String, ::String)
   @ Main.Notebook ~/Julia/23/Book-ansipatch/chapters/types.qmd:593

Stacktrace:
 [1] macro expansion
   @ show.jl:1232 [inlined]
 [2] top-level scope
   @ ~/Julia/23/Book-ansipatch/chapters/types.qmd:598
Wichtig

Explizite Typannotationen sind fast immer irrelevent für die Geschwindigkeit des Codes!

Dies ist einer der wichtigsten selling points von Julia.

Sobald eine Funktion zum ersten Mal mit bestimmten Typen aufgerufen wird, wird eine auf diese Argumenttypen spezialisierte Form der Funktion generiert und compiliert. Damit sind generische Funktionen in der Regel genauso schnell, wie die spezialisierten Funktionen, die man in anderen Sprachen schreibt.

Generische Funktionen erlauben die Zusammenarbeit unterschiedlichster Pakete und eine hohe Abstraktion.

Ein einfaches Beispiel: Das Paket Measurements.jl definiert einen neuen Datentyp Measurement, einen Wert mit Fehler, und die Arithmetik dieses Typs. Damit funktionieren generische Funktionen automatisch:

using Measurements

x = 33.56±0.3
y = 2.3±0.02

fsinnfrei1(x, y)
2590.0 ± 52.0

8.11 Typ-Parameter in Funktionsdefinitionen: die where-Klausel

Wir wollen eine Funktion schreiben, die für alle komplexen Integer (und nur diese) funktioniert, z.B. eine in ℤ[i] mögliche Primfaktorzerlegung. Die Definition

function isprime(x::Complex{Integer}) ... end

liefert nun nicht das Gewünschte, wie wir in Kapitel 8.9 gesehen haben. Die Funktion würde für ein Argument vom Typ Complex{Int64} nicht funktionieren, da letzteres kein Subtyp von Complex{Integer} ist.

Wir müssen eine Typ-Variable einführen. Dazu dient die where-Klausel.

function isprime(x::Complex{T}) where {T<:Integer}
     ... 
end

Das ist zu lesen als:

„Das Argument x soll von einem der Typen Complex{T} sein, wobei die Typvariable T irgendein Untertyp von Integer sein kann.“

Noch ein Beispiel:

function kgV(x::Complex{T}, y::Complex{S}) where {T<:Integer, S<:Integer}
     ... 
end

Die Argumente x und y können verschiedene Typen haben und beide müssen Subtypen von Integer sein.

Wenn es nur eine where-Klausel wie im vorletzten Beispiel gibt, kann man die geschweiften Klammern weglassen und

function isprime(x::Complex{T}) where T<:Integer
     ... 
end

schreiben. Das lässt sich noch weiter kürzen zu

function isprime(x::Complex{<:Integer}) 
     ... 
end

Diese verschiedenen Varianten können verwirrend sein, aber das ist nur Syntax.

C1 = Complex{T} where {T<:Integer} 
C2 = Complex{T} where T<:Integer
C3 = Complex{<:Integer}

C1 == C2 == C3
true

Kurze Syntax für einfache Fälle, ausführliche Syntax für komplexe Varianten.

Als letztes sein bemerkt, dass where T die Kurzform von where T<:Any ist, also eine völlig unbeschränkte Typvariable einführt. Damit ist sowas möglich:

function fgl(x::T, y::T) where T
    println("Glückwunsch! x und y sind vom gleichen Typ!")
end
fgl (generic function with 1 method)

Diese Methode erfordert, dass die Argumente genau den gleichen, aber ansonsten beliebigen Typ haben.

fgl(33, 44)
Glückwunsch! x und y sind vom gleichen Typ!
fgl(33, 44.0)
MethodError: no method matching fgl(::Int64, ::Float64)
The function `fgl` exists, but no method is defined for this combination of argument types.

Closest candidates are:
  fgl(::T, ::T) where T
   @ Main.Notebook ~/Julia/23/Book-ansipatch/chapters/types.qmd:721

Stacktrace:
 [1] top-level scope
   @ ~/Julia/23/Book-ansipatch/chapters/types.qmd:732