12 Vektoren, Matrizen, Arrays

12.1 Allgemeines

Kommen wir nun zu den wohl wichtigsten Containern für numerische Mathematik:

Vektoren Vector{T}
Matrizen Matrix{T} mit zwei Indizes
N-dimensionale Arrays mit N Indizes Array{T,N}

Tatsächlich ist Vector{T} ein Alias für Array{T,1} und Matrix{T} ein Alias für Array{T,2}.

Vector{Float64} === Array{Float64,1} && Matrix{Float64} ===  Array{Float64,2}

true

Beim Anlegen durch eine explizite Elementliste wird der ‘kleinste gemeinsame Typ’ für den Typparameter T ermittelt.

v = [33, "33", 1.2]

3-element Vector{Any}:
 33
   "33"
  1.2

Falls T ein numerischer Typ ist, werden die Elemente in diesen Typ umgewandelt.

v = [3//7, 4, 2im]

3-element Vector{Complex{Rational{Int64}}}:
 3//7 + 0//1*im
 4//1 + 0//1*im
 0//1 + 2//1*im

Informationen über einen Array liefern die Funktionen:

length(A) — Anzahl der Elemente
eltype(A) — Typ der Elemente
ndims(A) — Anzahl der Dimensionen (Indizes)
size(A) — Tupel mit den Dimensionen des Arrays

v1 = [12, 13, 15]

m1 = [ 1    2.5
       6    -3 ]

for f ∈ (length, eltype, ndims, size)
    println("$(f)(v) = $(f(v)),          $(f)(m1) = $(f(m1))")
end

length(v) = 3,          length(m1) = 4
eltype(v) = Complex{Rational{Int64}},          eltype(m1) = Float64
ndims(v) = 1,          ndims(m1) = 2
size(v) = (3,),          size(m1) = (2, 2)

Die Stärke des ‘klassischen’ Arrays für das wissenschaftliche Rechnen besteht darin, dass es einfach nur ein zusammenhängendes Speichersegment ist, in dem die Komponenten gleicher Länge (z.B. 64 Bit) geordnet hintereinander abgespeichert sind. Damit ist der Speicherbedarf minimal und die Zugriffsgeschwindigkeit auf eine Komponente, sowohl beim Lesen als auch beim Modifizieren, maximal. Der Platz der Komponente v[i] ist sofort aus i berechenbar.
Julias Array{T,N} (und damit Vektoren und Matrizen) ist für die üblichen numerischen Typen T in dieser Weise implementiert. Die Elemente werden unboxed gespeichert. Im Gegensatz dazu ist z.B. ein Vector{Any} implementiert als Liste von Adressen von Objekten (boxed) und nicht als Liste der Objekte selbst.
Julias Array{T,N} speichert seine Elemente direkt (unboxed), wenn isbitstype(T) == true.

isbitstype(Float64), 
isbitstype(Complex{Rational{Int64}}), 
isbitstype(String)

(true, true, false)

12.2 Vektoren

12.2.1 Listen-artige Funktionen

push!(vector, items...) — fügt Elemente am Ende des Vektors an
pushfirst!(vector, items...) — fügt Elemente am Anfang des Vektors an
pop!(vector) — entfernt letztes Element und liefert es als Ergebnis zurück,
popfirst!(vector) — entfernt erstes Element und liefert es zurück

v = Float64[]           # leerer Vector{Float64}

push!(v, 3, 7)
pushfirst!(v, 1)

a = pop!(v)
println("a= $a")

push!(v, 17)

a= 7.0

3-element Vector{Float64}:
  1.0
  3.0
 17.0

Ein push!() kann sehr aufwändig sein, da eventuell neuer Speicher alloziert und dann der ganze bestehende Vektor umkopiert werden muss. Julia optimiert das Speichermanagement. Es wird in einem solchen Fall Speicher auf Vorrat alloziert, so dass weitere push!s sehr schnell sind und man ‘fast O(1)-Geschwindigkeit’ erreicht.

Trotzdem sollte man bei zeitkritischem Code und sehr großen Feldern Operationen wie push!() oder resize() vermeiden.

12.2.2 Weitere Konstruktoren

Man kann Vektoren mit vorgegebener Länge und Typ uninitialisiert anlegen. Das geht am Schnellsten, die Elemente sind zufällige Bitmuster.

# fixe Länge 1000, uninitialisiert

v = Vector{Float64}(undef, 1000)
v[345]

5.27556352e-315

zeros(n) legt einen Vector{Float64} der Länge n an und initialisiert mit Null.

v = zeros(7)

7-element Vector{Float64}:
 0.0
 0.0
 0.0
 0.0
 0.0
 0.0
 0.0

zeros(T,n) legt einen Nullvektor vom Typ T an.

v=zeros(Int, 4)

4-element Vector{Int64}:
 0
 0
 0
 0

fill(x, n) legt Vector{typeof(x)} der Länge n an und füllt mit x.

v = fill(sqrt(2), 5)

5-element Vector{Float64}:
 1.4142135623730951
 1.4142135623730951
 1.4142135623730951
 1.4142135623730951
 1.4142135623730951

similar(v) legt einen uninitialisierten Vektor von gleichem Typ und Größe wie v an.

w = similar(v)

5-element Vector{Float64}:
 6.1793523506736e-310
 6.1793523506736e-310
 6.17935235067675e-310
 6.17935235112496e-310
 0.0

12.2.3 Konstruktion durch implizite Schleife (list comprehension)

Implizite for-Schleifen sind eine weitere Methode, Vektoren zu erzeugen.

v4 = [i for i in 1.0:8]

8-element Vector{Float64}:
 1.0
 2.0
 3.0
 4.0
 5.0
 6.0
 7.0
 8.0

v5 = [log(i^2) for i in 1:4 ]

4-element Vector{Float64}:
 0.0
 1.3862943611198906
 2.1972245773362196
 2.772588722239781

Man kann sogar noch ein if unterbringen.

v6 = [i^2 for i in 1:8 if i%3 != 2]

5-element Vector{Int64}:
  1
  9
 16
 36
 49

12.2.4 Bitvektoren

Neben Vector{Bool} gibt es noch den speziellen Datentyp BitVector (und allgemeiner auch BitArray) zur Speicherung von Feldern mit Wahrheitswerten.

Während für die Speicherung eines Bools ein Byte verwendet wird, erfolgt die Speicherung in einem BitVector bitweise.

Der Konstruktor wandelt einen Vector{Bool} in einen BitVector um.

vb = BitVector([true, false, true, true])

4-element BitVector:
 1
 0
 1
 1

Für die Gegenrichtung gibt es collect().

collect(vb)

4-element Vector{Bool}:
 1
 0
 1
 1

BitVectoren entstehen z.B. als Ergebnis von elementweisen Vergleichen (s. Kapitel 12.7).

v4 .> 3.5

8-element BitVector:
 0
 0
 0
 1
 1
 1
 1
 1

12.2.5 Indizierung

Indizes sind Ordinalzahlen. Also startet die Indexzählung mit 1.

Als Index kann man verwenden:

Integer
Integer-wertigen Range (gleiche Länge oder kürzer)
Integer-Vektor (gleiche Länge oder kürzer)
Bool-Vektor oder BitVector (gleiche Länge)

Mit Indizes kann man Arrayelemente/teile lesen und schreiben.

v = [ 3i + 5.2 for i in 1:8]

8-element Vector{Float64}:
  8.2
 11.2
 14.2
 17.2
 20.2
 23.2
 26.2
 29.2

v[5]

20.2

Bei Zuweisungen wird die rechte Seite wenn nötig mit convert(T,x) in den Vektorelementetyp umgewandelt.

v[6] = 9999
v

8-element Vector{Float64}:
    8.2
   11.2
   14.2
   17.2
   20.2
 9999.0
   26.2
   29.2

Überschreiten der Indexgrenzen führt zu einem BoundsError.

v[77]

BoundsError: attempt to access 8-element Vector{Float64} at index [77]
Stacktrace:
 [1] throw_boundserror(A::Vector{Float64}, I::Tuple{Int64})
   @ Base ./essentials.jl:14
 [2] getindex(A::Vector{Float64}, i::Int64)
   @ Base ./essentials.jl:916
 [3] top-level scope
   @ ~/Julia/23/Book-ansipatch/chapters/7_ArraysP2.qmd:214

Mit einem range-Objekt kann man einen Teilvektor adressieren.

vp = v[3:5]
vp

3-element Vector{Float64}:
 14.2
 17.2
 20.2

vp = v[1:2:7]   # range mit Schrittweite
vp

4-element Vector{Float64}:
  8.2
 14.2
 20.2
 26.2

Bei der Verwendung als Index kann in einem Range der Spezialwert end verwendet werden.
Bei der Verwendung als Index kann der “leere” Range : als Abkürzung von 1:end verwendet werden. Das ist nützlich bei Matrizen: A[:, 3] adressiert die gesamte 3. Spalte von A.

v[6:end] = [7, 7, 7]
v

8-element Vector{Float64}:
  8.2
 11.2
 14.2
 17.2
 20.2
  7.0
  7.0
  7.0

Indirekte Indizierung

Die indirekte Indizierung mit einem Vector of Integers/Indices erfolgt nach der Formel

\(v[ [i_1,\ i_2,\ i_3,...]] = [\ v[i_1],\ v[i_2],\ v[i_3],...]\)

v[ [1, 3, 4] ]

3-element Vector{Float64}:
  8.2
 14.2
 17.2

ist also gleich

[ v[1], v[3], v[4] ]

3-element Vector{Float64}:
  8.2
 14.2
 17.2

Indizierung mit einem Vektor von Wahrheitswerten

Als Index kann man auch einen Vector{Bool} oder BitVector (s. Kapitel 12.2.4) derselben Länge verwenden.

v[ [true, true, false, false, true, false, true, true] ]

5-element Vector{Float64}:
  8.2
 11.2
 20.2
  7.0
  7.0

Das ist nützlich, da man z.B.

Tests broadcasten kann (s. Kapitel 12.7),
diese Tests dann einen BitVector liefern und
bei Bedarf solche Bitvektoren durch die Bit-weisen Operatoren & und | verknüpft werden können.

v[  (v .> 13) .& (v.<20) ]

2-element Vector{Float64}:
 14.2
 17.2

12.3 Matrizen und Arrays

Die bisher vorgestellten Methoden für Vektoren übertragen sich auch auf höherdimensionale Arrays.

Man kann sie uninitialisiert anlegen:

A = Array{Float64,3}(undef, 6,9,3)

6×9×3 Array{Float64, 3}:
[:, :, 1] =
 1.0e-323      1.5e-323      2.0e-323  …  5.4e-323      7.0e-323
 5.0e-324      1.0e-323      1.5e-323     4.4e-323      5.4e-323
 6.17933e-310  6.17933e-310  5.0e-324     6.17935e-310  6.17934e-310
 7.0e-323      7.0e-323      3.0e-323     6.0e-323      6.17935e-310
 1.0e-323      1.5e-323      2.0e-323     5.0e-323      6.17935e-310
 6.17933e-310  0.0           5.0e-324  …  6.17935e-310  6.17935e-310

[:, :, 2] =
 6.17935e-310  6.17935e-310  6.17935e-310  …  6.17935e-310  6.17934e-310
 6.17935e-310  6.17935e-310  6.17935e-310     6.17935e-310  6.17935e-310
 6.17935e-310  6.17935e-310  6.17935e-310     6.17936e-310  6.17934e-310
 6.17935e-310  6.17935e-310  6.17935e-310     6.17935e-310  6.17935e-310
 6.17935e-310  6.17935e-310  6.17935e-310     6.17936e-310  6.17936e-310
 6.17935e-310  6.17935e-310  6.17935e-310  …  6.17935e-310  6.17935e-310

[:, :, 3] =
 6.17934e-310  6.17936e-310  5.0e-324      …  5.4e-323      1.63e-322
 6.17935e-310  6.17935e-310  0.0              4.4e-323      5.4e-323
 6.17935e-310  6.17936e-310  5.0e-324         5.0e-324      6.17935e-310
 6.17935e-310  6.17935e-310  1.0e-323         6.0e-323      6.4e-323
 6.17936e-310  2.03e-322     5.0e-324         5.0e-323      5.4e-323
 6.17935e-310  6.17933e-310  2.75859e-313  …  6.17935e-310  6.17935e-310

In den meisten Funktionen kann man die Dimensionen auch als Tupel übergeben. Die obige Anweisung lässt sich auch so schreiben:

A = Array{Float64, 3}(undef, (6,9,3))

Funktionen wie zeros() usw. funktionieren natürlich auch.

m2 = zeros(3, 4, 2)  # oder zeros((3,4,2))

3×4×2 Array{Float64, 3}:
[:, :, 1] =
 0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0

[:, :, 2] =
 0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0

M = fill(5 , (3, 3))   # oder fill(5, 3, 3)

3×3 Matrix{Int64}:
 5  5  5
 5  5  5
 5  5  5

Die Funktion similar(), die einen Array gleicher Größe uninitialisiert erzeugt, kann auch einen Typ als weiteres Argument bekommen.

M2 = similar(M, Float64)

3×3 Matrix{Float64}:
 6.17935e-310  6.17935e-310  6.17935e-310
 6.17935e-310  6.17935e-310  6.17935e-310
 6.17935e-310  6.17935e-310  6.17935e-310

12.3.1 Konstruktion durch explizite Elementliste

Während man Vektoren kommagetrennt in eckigen Klammern notiert, ist die Notation für höherdimensionale Objekte etwas anders.

Eine Matrix:

M2 = [2  3  -1
      4  5  -2]

2×3 Matrix{Int64}:
 2  3  -1
 4  5  -2

dieselbe Matrix:

M2 = [2 3 -1; 4 5 -2]

2×3 Matrix{Int64}:
 2  3  -1
 4  5  -2

Ein Array mit 3 Indizes:

M3 = [2   3  -1 
      4   5   6 ;;;
      7   8   9
     11  12  13]

2×3×2 Array{Int64, 3}:
[:, :, 1] =
 2  3  -1
 4  5   6

[:, :, 2] =
  7   8   9
 11  12  13

und nochmal die Matrix M2:

M2 = [2;4;; 3;5;; -1;-2]

2×3 Matrix{Int64}:
 2  3  -1
 4  5  -2

Im letzten Beispiel kommen diese Regeln zur Anwendung:

Trenner ist das Semikolon.
Ein Semikolon ; erhöht den 1. Index.
Zwei Semikolons ;; erhöhen den 2. Index.
Drei Semikolons ;;; erhöhen den 3. Index usw.

In den Beispielen davor wurde folgende Syntaktische Verschönerung (syntactic sugar) angewendet:

Leerzeichen trennen wie 2 Semikolons – erhöht also den 2. Index: \(\quad a_{12}\quad a_{13}\quad a_{14}\ ...\)
Zeilenumbruch trennt wie ein Semikolon – erhöht also den 1. Index.

Wichtig

Vektorschreibweise mit Komma als Trenner geht nur bei Vektoren, nicht mit “Semikolon, Leerzeichen, Newline” mischen!
Vektoren, \(1\!\times\!n\)-Matrizen und \(n\!\times\!1\)-Matrizen sind drei verschiedene Dinge!

v1 = [2,3,4]

3-element Vector{Int64}:
 2
 3
 4

v2 = [2;3;4]

3-element Vector{Int64}:
 2
 3
 4

v3 = [2 3 4]

1×3 Matrix{Int64}:
 2  3  4

v3 = [2;3;4;;]

3×1 Matrix{Int64}:
 2
 3
 4

Einen “vector of vectors” a la C/C++ kann man natürlich auch konstruieren.

v = [[2,3,4], [5,6,7,8]]

2-element Vector{Vector{Int64}}:
 [2, 3, 4]
 [5, 6, 7, 8]

v[2][3]

Das sollte man nur in Spezialfällen tun. Die Array-Sprache von Julia ist in der Regel bequemer und schneller.

12.3.2 Indizes, Teilfelder, Slices

# 6x6 Matrix mit Zufallszahlen gleichverteilt aus [0,1) ∈ Float64
A = rand(6,6)

6×6 Matrix{Float64}:
 0.169398    0.452612    0.475178  0.904675  0.94847   0.714828
 0.351193    0.00174175  0.902776  0.395178  0.914661  0.416559
 0.00109605  0.16115     0.353172  0.527975  0.751782  0.562037
 0.0223763   0.998882    0.336013  0.959604  0.771769  0.0474043
 0.862148    0.214111    0.211747  0.140627  0.987201  0.279285
 0.308576    0.641049    0.229695  0.20216   0.700358  0.940126

Die übliche Indexnotation:

A[2, 3] = 77.77777
A

6×6 Matrix{Float64}:
 0.169398    0.452612     0.475178  0.904675  0.94847   0.714828
 0.351193    0.00174175  77.7778    0.395178  0.914661  0.416559
 0.00109605  0.16115      0.353172  0.527975  0.751782  0.562037
 0.0223763   0.998882     0.336013  0.959604  0.771769  0.0474043
 0.862148    0.214111     0.211747  0.140627  0.987201  0.279285
 0.308576    0.641049     0.229695  0.20216   0.700358  0.940126

Man kann mit Ranges Teilfelder adressieren:

B = A[1:2, 1:3]

2×3 Matrix{Float64}:
 0.169398  0.452612     0.475178
 0.351193  0.00174175  77.7778

Das Adressieren von Teilen mit geringerer Dimension wird auch slicing genannt.

# die 3. Spalte als Vektor (slicing)

C = A[:, 3]

6-element Vector{Float64}:
  0.4751777214121483
 77.77777
  0.3531723977012804
  0.33601322076700646
  0.21174688880149883
  0.22969544744803772

# die 3. Zeile als Vektor (slicing)

E = A[3, :]

6-element Vector{Float64}:
 0.0010960453817544513
 0.16114953399420406
 0.3531723977012804
 0.52797520667903
 0.7517819137326569
 0.5620369628617311

Natürlich sind damit auch Zuweisungen möglich:

# Man kann slices und Teilfeldern auch etwas zuweisen 

A[2, :] = [1,2,3,4,5,6]
A

6×6 Matrix{Float64}:
 0.169398    0.452612  0.475178  0.904675  0.94847   0.714828
 1.0         2.0       3.0       4.0       5.0       6.0
 0.00109605  0.16115   0.353172  0.527975  0.751782  0.562037
 0.0223763   0.998882  0.336013  0.959604  0.771769  0.0474043
 0.862148    0.214111  0.211747  0.140627  0.987201  0.279285
 0.308576    0.641049  0.229695  0.20216   0.700358  0.940126

12.4 Verhalten bei Zuweisungen, `copy()` und `deepcopy()`, Views

12.4.1 Zuweisungen und Kopien

Variablen sind Referenzen auf Objekte.
Eine Zuweisung zu einer Variablen erzeugt kein neues Objekt.

A = [1, 2, 3]
B = A

3-element Vector{Int64}:
 1
 2
 3

A und B sind jetzt Namen desselben Objekts.

A[1] = 77
@show B;

B = [77, 2, 3]

B[3] = 300
@show A;

A = [77, 2, 300]

Dieses Verhalten spart viel Zeit und Speicher, ist aber nicht immer gewünscht. Die Funktion copy() erzeugt eine ‘echte’ Kopie des Objekts.

A = [1, 2, 3]
B = copy(A)
A[1] = 100
@show A B;

A = [100, 2, 3]
B = [1, 2, 3]

Die Funktion deepcopy(A) kopiert rekursiv. Auch von den Elementen, aus denen A besteht, werden (wieder rekursive) Kopien erstellt.

Solange ein Array nur primitive Objekte (Zahlen) enthält, sind copy() und deepcopy() äquivalent.

Das folgende Beispiel zeigt den Unterschied zwischen copy() und deepcopy().

mutable struct Person
    name :: String
    age  :: Int
end

A = [Person("Meier", 20), Person("Müller", 21), Person("Schmidt", 23)]
B = A
C = copy(A)
D = deepcopy(A)

3-element Vector{Person}:
 Person("Meier", 20)
 Person("Müller", 21)
 Person("Schmidt", 23)

A[1] = Person("Mustermann", 83)
A[3].age = 199 

@show B C D;

B = Main.Notebook.Person[Main.Notebook.Person("Mustermann", 83), Main.Notebook.Person("Müller", 21), Main.Notebook.Person("Schmidt", 199)]
C = Main.Notebook.Person[Main.Notebook.Person("Meier", 20), Main.Notebook.Person("Müller", 21), Main.Notebook.Person("Schmidt", 199)]
D = Main.Notebook.Person[Main.Notebook.Person("Meier", 20), Main.Notebook.Person("Müller", 21), Main.Notebook.Person("Schmidt", 23)]

12.4.2 Views

Wenn man mittels indices/ranges/slices einer Variablen ein Teilstück eines Arrays zuweist, wird von Julia grundsätzlich ein neues Objekt konstruiert.

A = [1  2  3
     3  4  5]

v = A[:, 2]
@show  v

A[1, 2] = 77
@show  A  v;

v = [2, 4]
A = [1 77 3; 3 4 5]
v = [2, 4]

Manchmal möchte man aber gerade hier eine Referenz-Semantik haben im Sinne von: “Vektor v soll der 2. Spaltenvektor von A sein und auch bleiben (d.h., sich mitändern, wenn sich A ändert).”

Dies bezeichnet man in Julia als views: Wir wollen, dass die Variable v nur einen ‘alternativen Blick’ auf die Matrix A darstellt.

Das kann man erreichen durch das @view-Macro:

A = [1 2 3
     3 4 5]

v = @view A[:,2]
@show  v

A[1, 2] = 77
@show  v;

v = [2, 4]
v = [77, 4]

Diese Technik wird von Julia aus Effizienzgründen auch bei einigen Funktionen der linearen Algebra verwendet. Ein Beispiel ist der Operator ', der zu einer Matrix A die adjungierte Matrix A' liefert.

Die adjungierte (adjoint) Matrix A' ist die transponierte und elementweise komplex-konjugierte Matrix zu A.
Der Parser macht daraus den Funktionsaufruf adjoint(A).
Für reelle Matrizen ist die Adjungierte gleich der transponierten Matrix.
Julia implementiert adjoint() als lazy function, d.h.,
es wird aus Effizienzgründen kein neues Objekt konstruiert, sondern nur ein alternativer ‘View’ auf die Matrix (“mit vertauschten Indizes”) und ein alternativer ‘View’ auf die Einträge (mit Vorzeichenwechsel im Imaginärteil).
Aus Vektoren macht adjoint() eine \(1\!\times\!n\)-Matrix (einen Zeilenvektor).

A = [ 1.  2.
      3.  4.]
B = A'

2×2 adjoint(::Matrix{Float64}) with eltype Float64:
 1.0  3.0
 2.0  4.0

Die Matrix B ist nur ein modifizierter ‘View’ auf A:

A[1, 2] =10
B

2×2 adjoint(::Matrix{Float64}) with eltype Float64:
  1.0  3.0
 10.0  4.0

Aus Vektoren macht adjoint() eine \(1\!\times\!n\)-Matrix (einen Zeilenvektor).

v = [1, 2, 3]
v'

1×3 adjoint(::Vector{Int64}) with eltype Int64:
 1  2  3

Eine weitere solche Funktion, die einen alternativen ‘View’, eine andere Indizierung, derselben Daten liefert, ist reshape().

Hier wird ein Vektor mit 12 Einträgen in eine 3x4-Matrix verwandelt.

A = [1,2,3,4,5,6,7,8,9,10,11,12]

B = reshape(A, 3, 4)

3×4 Matrix{Int64}:
 1  4  7  10
 2  5  8  11
 3  6  9  12

12.5 Speicherung eines Arrays

Speicher wird linear adressiert. Eine Matrix kann zeilenweise (row major) oder spaltenweise (column major) im Speicher angeordnet sein.
C/C++/Python(NumPy) verwenden eine zeilenweise Speicherung: Die 4 Elemente einer 2x2-Matrix sind abgespeichert in der Reihenfolge \(a_{11},a_{12},a_{21},a_{22}\).
Julia, Fortran, Matlab speichern spaltenweise: \(a_{11},a_{21},a_{12},a_{22}\).

Diese Information ist wichtig, um effizient über Matrizen zu iterieren:

function column_major_add(A, B)
    (n,m) = size(A)
    for j = 1:m
        for i = 1:n     # innere Schleife durchläuft eine Spalte
            A[i,j] += B[i,j]
        end
    end
end

function row_major_add(A, B)
    (n,m) = size(A)
    for i = 1:n
        for j = 1:m     # inere Schleife durchläuft eine Zeile
            A[i,j] += B[i,j]
        end
    end
end

row_major_add (generic function with 1 method)

A = rand(10000, 10000);
B = rand(10000, 10000);

using BenchmarkTools

@benchmark row_major_add($A, $B)

BenchmarkTools.Trial: 5 samples with 1 evaluation per sample.
 Range (min … max):  989.481 ms …   1.035 s  ┊ GC (min … max): 0.00% … 0.00%
 Time  (median):        1.005 s              ┊ GC (median):    0.00%
 Time  (mean ± σ):      1.008 s ± 18.607 ms  ┊ GC (mean ± σ):  0.00% ± 0.00%

  █    █              █                  █                   █  
  █▁▁▁▁█▁▁▁▁▁▁▁▁▁▁▁▁▁▁█▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁█▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁█ ▁
  989 ms          Histogram: frequency by time          1.03 s <

 Memory estimate: 0 bytes, allocs estimate: 0.

@benchmark column_major_add($A, $B)

BenchmarkTools.Trial: 61 samples with 1 evaluation per sample.
 Range (min … max):  69.358 ms … 249.199 ms  ┊ GC (min … max): 0.00% … 0.00%
 Time  (median):     72.889 ms               ┊ GC (median):    0.00%
 Time  (mean ± σ):   83.290 ms ±  31.111 ms  ┊ GC (mean ± σ):  0.00% ± 0.00%

  ▇█▄                                                           
  ███▅▄▃▃▄▄▁▁▁▁▁▃▁▁▁▃▁▃▁▁▁▁▁▁▃▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▃▁▁▁▁▁▁▃▁▁▁▁▁▃ ▁
  69.4 ms         Histogram: frequency by time          181 ms <

 Memory estimate: 0 bytes, allocs estimate: 0.

12.5.1 Lokalität von Speicherzugriffen und Caching

Wir haben gesehen, dass die Reihenfolge von innerem und äußerem Loop einen erheblichen Geschwindigkeitsunterschied macht:

Es ist effizienter, wenn die innerste Schleife über den linken Index läuft, also eine Spalte und nicht eine Zeile durchläuft. Die Ursache dafür liegt in der Architektur moderner Prozessoren.

Speicherzugriffe erfolgt über mehrere Cache-Ebenen.
Ein cache miss, der ein Nachladen aus langsameren Caches auslöst, bremst aus.
Es werden immer gleich größere Speicherblöcke nachgeladen, um die Häufigkeit von cache misses zu minimieren.
Daher ist es wichtig, Speicherzugriffe möglichst lokal zu organisieren.

Speicherhierarchie von Intel-Prozessoren, aus: Victor Eijkhout,*Introduction to High-Performance Scientific Computing*, https://theartofhpc.com/

12.6 Mathematische Operationen mit Arrays

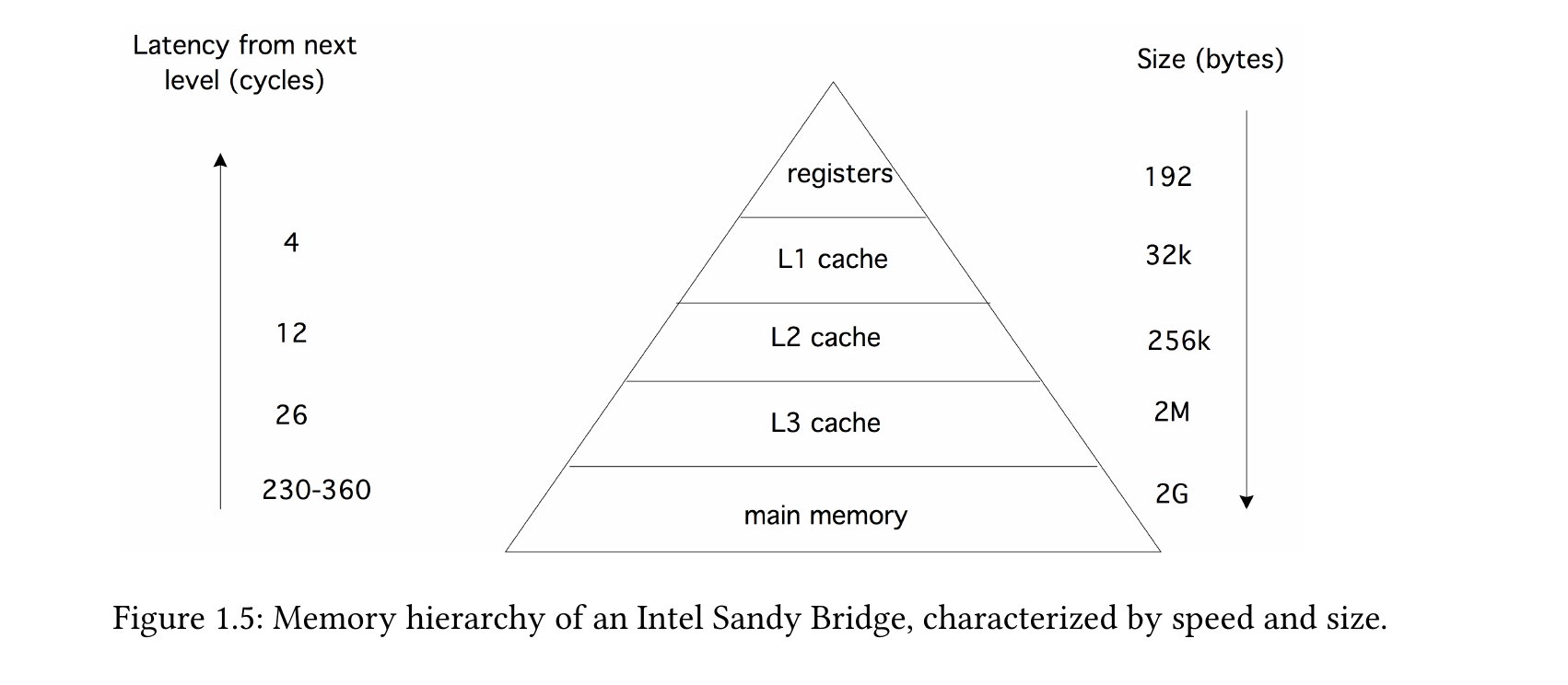
Arrays der gleichen Dimension (z.B. alle \(7\!\times\!3\)-Matrizen) bilden einen linearen Raum.

Sie können mit Skalaren multipliziert werden und
sie können addiert und subtrahiert werden.

0.5 * [2, 3, 4, 5]

4-element Vector{Float64}:
 1.0
 1.5
 2.0
 2.5

0.5 * [ 1  3
        2  7] - [ 2  3; 1 2]

2×2 Matrix{Float64}:
 -1.5  -1.5
  0.0   1.5

12.6.1 Matrixprodukt

Das Matrixprodukt ist definiert für

1. Faktor	2. Faktor	Produkt
\((n\!\times\!m)\)-Matrix	\((m\!\times\!k)\)-Matrix	\((n\times k)\)-Matrix
\((n\!\times\!m)\)-Matrix	\(m\)-Vektor	\(n\)-Vektor
\((1\!\times\!m)\)-Zeilenvektor	\((m\!\times\!n)\)-Matrix	\(n\)-Vektor
\((1\!\times\!m)\)-Zeilenvektor	\(m\)-Vektor	Skalarprodukt
\(m\)-Vektor	\((1\times n)\)-Zeilenvektor	\((m\!\times\!n)\)-Matrix

Beispiele:

A = [1 2 3
     4 5 6]
v = [2, 3]
w = [1, 3, 4];

(2,3)-Matrix * (3,2)-Matrix

A * A'

2×2 Matrix{Int64}:
 14  32
 32  77

(3,2)-Matrix * (2,3)-Matrix

A' * A

3×3 Matrix{Int64}:
 17  22  27
 22  29  36
 27  36  45

(2,3)-Matrix * 3-Vektor

A * w

2-element Vector{Int64}:
 19
 43

(1,2)-Vektore * (2,3)-Matrix

v' * A

1×3 adjoint(::Vector{Int64}) with eltype Int64:
 14  19  24

(3,2)-Matrix * 2-Vektor

A' * v

3-element Vector{Int64}:
 14
 19
 24

(1,2)-Vektor * 2-Vektor (Skalarprodukt)

v' * v

2-Vektor * (1,3)-Vektor (äußeres Produkt)

v * w'

2×3 Matrix{Int64}:
 2  6   8
 3  9  12

12.7 Broadcasting

Beim broadcasting werden Operationen oder Funktionen elementweise auf Arrays angewendet.
Die Syntax dafür ist ein Punkt vor einem Operationszeichen oder nach einem Funktionsnamen.
Der Parser setzt f.(x,y) um zu broadcast(f, x, y) und analog für Operatoren x .⊙ y zu broadcast(⊙, z, y).
Dabei werden Operanden, denen eine oder mehrere Dimensionen fehlen, in diesen Dimensionen (virtuell) vervielfältigt.
Das broadcasting von Zuweisungen .=, .+=,… verändert die Semantik. Es wird kein neues Objekt erzeugt, sondern die Werte werden in das links stehende Objekt (welches die richtige Dimension haben muss) eingetragen.

Einige Beispiele:

Elementweise Anwendung einer Funktion

sin.([1, 2, 3])

3-element Vector{Float64}:
 0.8414709848078965
 0.9092974268256817
 0.1411200080598672

Das Folgende liefert nicht die algebraische Wurzel aus einer Matrix, sondern die elementweise Wurzel aus jedem Eintrag.

A = [8 2
     3 4]

sqrt.(A)

2×2 Matrix{Float64}:
 2.82843  1.41421
 1.73205  2.0

Das Folgende liefert nicht \(A^2\), sondern die Einträge werden quadriert.

A.^2

2×2 Matrix{Int64}:
 64   4
  9  16

Zum Vergleich das Ergebnis der algebraischen Operationen:

@show A^2 A^(1/2);

A ^ 2 = [70 24; 36 22]
A ^ (1 / 2) = [2.780234855920959 0.42449510866609885; 0.6367426629991483 1.9312446385887614]

Broadcasting geht auch mit Funktionen mehrerer Variablen.

hyp(a,b) = sqrt(a^2+b^2)

B = [3 4
     5 7]

hyp.(A, B)

2×2 Matrix{Float64}:
 8.544    4.47214
 5.83095  8.06226

Bei Operanden verschiedener Dimension wird der Operand mit fehlenden Dimensionen in diesen durch Vervielfältigung virtuell ‘aufgeblasen’.

Wir addieren einen Skalar zu einer Matrix:

A = [ 1 2 3
      4 5 6]

2×3 Matrix{Int64}:
 1  2  3
 4  5  6

A .+ 300

2×3 Matrix{Int64}:
 301  302  303
 304  305  306

Der Skalar wurde durch Replikation auf dieselbe Dimension wie die Matrix gebracht. Wir lassen uns von broadcast() die Form des 2. Operanden nach dem broadcasting anzeigen:

broadcast( (x,y) -> y, A, 300)

2×3 Matrix{Int64}:
 300  300  300
 300  300  300

(Natürlich findet diese Replikation nur virtuell statt. Dieses Objekt wird bei anderen Operationen nicht wirklich erzeugt.)

Als weiteres Beispiel: Matrix und (Spalten-)Vektor

A .+ [10, 20]

2×3 Matrix{Int64}:
 11  12  13
 24  25  26

Der Vektor wird durch Wiederholung der Spalten aufgeblasen:

broadcast((x,y)->y, A, [10,20])

2×3 Matrix{Int64}:
 10  10  10
 20  20  20

Matrix und Zeilenvektor: Der Zeilenvektor wird zeilenweise vervielfältigt:

A .* [1,2,3]'      # Adjungierter Vektor

2×3 Matrix{Int64}:
 1   4   9
 4  10  18

Der 2. Operand wird von broadcast() durch Vervielfältigung der Zeilen ‘aufgeblasen’.

broadcast((x,y)->y, A, [1,2,3]')

2×3 Matrix{Int64}:
 1  2  3
 1  2  3

Broadcasting bei Zuweisungen

Zuweisungen =, +=, /=,…, bei denen links ein Name steht, laufen in Julia so ab, dass aus der rechten Seite ein Objekt konstruiert und diesem Objekt der neue Name zugewiesen wird.

Beim Arbeiten mit Arrays will man allerdings sehr oft aus Effizienzgründen einen bestehenden Array weiterverwenden. Die rechts berechneten Einträge sollen in das bereits existierende Objekt auf der linken Seite eingetragen werden.

Das erreicht man mit den Broadcast-Varianten .=, .+=,… der Zuweisungsoperatoren.

A .= 3

2×3 Matrix{Int64}:
 3  3  3
 3  3  3

A .+= [1, 4]

2×3 Matrix{Int64}:
 4  4  4
 7  7  7

12.8 Weitere Array-Funktionen - eine Auswahl

Julia stellt eine große Anzahl von Funktionen bereit, die mit Arrays arbeiten.

A = [22 -17 8 ; 4 6 9]

2×3 Matrix{Int64}:
 22  -17  8
  4    6  9

Finde das Maximum

maximum(A)

Finde das Maximum jeder Spalte

maximum(A, dims=1)

1×3 Matrix{Int64}:
 22  6  9

Finde das Maximum jeder Zeile

maximum(A, dims=2)

2×1 Matrix{Int64}:
 22
  9

Finde das Minimum und seine Position

amin, i = findmin(A)

(-17, CartesianIndex(1, 2))

Was ist ein CartesianIndex?

dump(i)

CartesianIndex{2}
  I: Tuple{Int64, Int64}
    1: Int64 1
    2: Int64 2

Extrahiere die Indizes des Minimum als Tupel

i.I

(1, 2)

Summe und Produkt aller Einträge

sum(A), prod(A)

(32, -646272)

Spaltensumme (1. Index wird reduziert)

sum(A, dims=1)

1×3 Matrix{Int64}:
 26  -11  17

Zeilensummen (2. Index wird reduziert)

sum(A, dims=2)

2×1 Matrix{Int64}:
 13
 19

Summiere nach elementweiser Anwendung einer Funktion

sum(x->sqrt(abs(x)), A)   #   sum_ij sqrt(|a_ij|)

19.09143825297046

Reduziere (falte) den Array mit einer Funktion

reduce(+, A)    #  equivalent to sum(A)

mapreduce(f, op, array): Wende f auf alle Einträge an, dann reduziere mit op


mapreduce(x -> x^2, +, A )     # Summe der Quadrate aller Einträge

Gibt es Elemente in A, die > 5 sind?

any(x -> x>5, A)

true

Wieviele Elemente in A sind > 5?

count(x-> x>5, A)

sind alle Einträge positiv?

all(x-> x>0, A)

false