Ich denke mal, die Freude über Ihre erste Direct3D-Anwendung wird ein wenig getrübt sein durch die Tatsache, dass an der 3D-Anwendung gar nicht soviel dreidimensionales dran ist. Mal ehrlich, das hätten wir auch wesentlich einfacher haben können, oder? Naja, für simple 2D-Anwendungen ist DirectXGraphics ja auch nicht gedacht. Die vielen Einstellungen, Parameter und Funktionen, die wir in den letzten Kapiteln benutzt haben, dienen dem Grundsatz, sich alle Möglichkeiten in der dritten Dimension offenhalten zu können. Und mit ein paar dieser Möglichkeiten werden wir uns in diesem Kapitel beschäftigen.
In diesem Kapitel lernen Sie, wie man Körper dreidimensional erscheinen lässt. Darüberhinaus werden wir uns mit den Grundelementen der Animationstechnik befassen. Ausserdem werden wir den Tiefenbuffer (auch Z-Buffer genannt) kennenlernen, mit dem wir sicherstellen, dass Objekte im Hintegrund nicht versehentlich Objekte im Vordergrund überlappen. Auch dieses Kapitel ist mal wieder verknüpft mit einem Beispielprogramm, das wir von Abschnitt zu Abschnitt zusammenbauen werden. Diesmal stellen wir zwei Zylinder dar, von denen einer rotiert.
Den linken Zylinder werden wir zudem auch noch ein wenig stauchen. Beiden Zylindern gemeinsam ist die Tatsache, dass ihre Vertices im selben Vertexbuffer enthalten sind. Damit lernen Sie ein ganz wesentliches Element des Programmierens in 3D kennen. Wenn Sie mehrmals das gleiche 3D-Objekt darstellen wollen, benötigen Sie immer nur einen Vertexbuffer. Die Koordinaten werden durch Matrizen lediglich transformiert. Desweiteren werden wir den beiden Zylindern einen Schatten geben. Ein kleiner Kameraflug um diese beiden Zylinder peppt die Sache noch ein wenig auf.
Bevor wir uns mit den verschiedenen Arten der Transformation befassen, will ich Ihnen nur kurz den Algorithmus für die Erstellung des Zylinders zeigen:
// Diese Funktion dient uns lediglich dazu, die Eingabe der Daten zu erleichtern
function GetCustomVertex(_x, _y, _z: single; _color: TD3DColor): CUSTOMVERTEX;
begin
with Result do
begin
x := _x;
y := _y;
z := _z;
color := _color;
end;
end;
procedure InitGeometry;
var
Vertices: Array[0..99] of CUSTOMVERTEX;
cx: Integer;
theta: Single;
pVertices : PByte;
begin
// Erstellen der Vertex-Koordinaten für einen Zylinder
for cx := 0 to 49 do
begin
theta := ( 2 * D3DX_PI * cx ) /49;
Vertices[ 2 * cx ] := GetCustomVertex(sin( theta ), -1.0, cos( theta ), $FF00FF00);
Vertices[ 2 * cx + 1 ] := GetCustomVertex(sin( theta ), 1.0, cos( theta ), $FFFF0000);
end;
// Erstellen des Vertexbuffers
if ( d3ddev8.CreateVertexBuffer( sizeof( CUSTOMVERTEX ) * 100, 0, D3DFVF_CUSTOMVERTEX,
D3DPOOL_DEFAULT, vbuffer ) <> D3D_OK ) then Exit;
if ( vbuffer.Lock( 0, sizeof( Vertices ), pVertices, 0 ) <> D3D_OK ) then Exit;
Move( Vertices, pVertices^, sizeof( Vertices ) );
vbuffer.Unlock;
end;
|
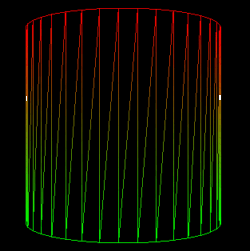
Wir greifen hierbei das Vertexformat aus dem Kapitel 
Der Vertexbuffer auf. Diesmal erstellen wir 100 Vertices, damit der Zylinder auch schön rund wirkt. Die Vertices werden jeweils um den Nullpunkt herum angeordnet und zwar jeweils immer ein Vertex mit der Höhe -1 und ein Vertex mit der Höhe +1. Unser Zylinder hat also insgesamt 50 Ecken.
Der Aufbau des Zylinders wird recht deutlich an dem unteren Bild, bei dem man nur die Vorderseite des Zylinders sieht. Damit das Drahtgittermodell deutlicher wird, habe ich die Vertex-Zahl für diesen Screenshot ein wenig verringert.
Die Art und Weise, wie wir ein 3D-Objekt sehen ist abhängig von vier Dingen:
All diese Dinge können wir beeinflussen, und zwar mit Matrizen. Wenn Sie nicht wissen, was Matrizen sind, dann sollten Sie an dieser Stelle einen Blick in das Kapitel Matrizen werfen. In dem wir also in die Matrizenfelder die entsprechenden Zahlen eingeben, und diese Matrizen dann dem Device übergeben, können wir ein 3D-Objekt perspektivisch korrekt, so, wie wir es wünschen, betrachten. Die Übergabe der Matrizen für die vier entscheidenden Faktoren erfolgt mit der .SetTransform-Funktion des Devices:
function SetTransform(const State : TD3DTransformStateType;
const pMatrix : TD3DMatrix) : HResult;
|
State: Hier geben Sie an, was Sie transformieren wollen. Verwenden Sie hierzu eine Konstante der D3DTransformStateType-Aufzählungen. Sie können unter anderem zwischen der Kamera-, Textur-, und Welttransformierung wählen.
pMatrix: Die Matrix, die die Transformierungszahlen enthält. Sie ist vom Typ D3DMatrix oder D3DXMatrix.
Um vorhandene Matrizeneinstellungen erweitern zu können, können Sie sich diese ausgeben lassen. Der Befehl dafür sieht ganz ähnlich aus, mit dem Unterschied, dass die Matrix, die als Parameter übergeben wird, mit den entsprechenden Daten gefüllt wird.
function GetTransform(const State : TD3DTransformStateType;
out pMatrix : TD3DMatrix) : HResult;
|
Die nachfolgenden Abschnitte beschäftigen sich damit, wie man die richtigen Zahlen der Matrix übergibt.
Nehmen wir uns zuerst die View-, und die Projection-Matrix vor. Letzteres beinhaltet sozusagen die Einstellungen der Linse, durch die wir gucken. Eine der möglichen Einstellungen ist der Sichtwinkel, also der Umfang dessen, was wir sehen können. Betrachten Sie dazu folgende beiden Skizzen:
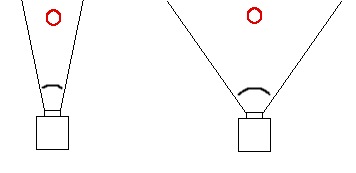
Zwei Kameras betrachten einen Zylinder aus der gleichen Entfernung, jedoch mit einem wesentlichen Unterschied. Die linke Kamera hat einen wesentlich kleineren Sichtwinkel, als die rechte. Demzufolge erscheint der Zylinder mit der linken Kamera näher, als mit der rechten, weil er grösser dargestellt wird, obwohl in beiden Fällen der Zylinder den gleichen Abstand zur Kamera hat. Das nachfolgende Bild macht dieses Phänomen an einem Flugzeug deutlich.
Da der Sichtwinkel bei der rechten Kamera grösser ist, ist auch die Fläche grösser, die auf den Bildschirm untergebracht werden muss. Demzufolge erscheinen die Dinge kleiner. Der Normalwinkel für eine realitätsnahe Darstellung liegt bei PI / 4. Das ist in etwa der Sichtwinkel, den wir beim Blick auf den Bildschirm haben.
In der Projektionsmatrix lassen sich noch weitere Dinge einstellen, die nachfolgend erklärt werden. Zum einfachen Erstellen der Projektionsmatrix gibt es zwei Befehle, die Ihnen bei der Eingabe helfen. Fügen Sie dazu in der USES-Klausel Ihrer Anwendung d3dx8 ein. Diese Unit beinhaltet viele nütliche Funktionen, die DirectXGraphics unterstützt.
function D3DXMatrixPerspectiveLH( out MOut: TD3DXMatrix;
w: Single;
h: Single;
zn: Single;
zf: Single;
);
|
MOut: Eine Variable vom Typ D3DXMatrix, die mit den entsprechenden Zahlen gefüllt wird.
w: Die Breite des sichtbaren Bereiches bei zn.
h: Die Höhe des sichtbaren Bereiches bei zn.
zn: Ab welcher Tiefe von der Kamera ausgehend Vertices bzw. Dreiecke sichtbar sein sollen.
zf: Ab welcher Tiefe von der Kamera ausgehend Vertices bzw. Dreiecke nicht mehr sichtbar sein sollen.
In dieser Funktion wird also der Sichtwinkel mit den Variablen w und h eingestellt. Anders ist das bei der zweiten Funktion, die Sie statt D3DXMatrixPerspectiveLH() verwenden können:
function D3DXMatrixPerspectivePovLH( out MOut: TD3DXMatrix;
fovy: Single;
Aspect: Single;
zn: Single;
zf: Single;
);
|
MOut: Eine Variable vom Typ D3DXMatrix, die mit den entsprechenden Zahlen gefüllt wird.
fovy: der oben angesprochene Sichtwinkel, als radialer Wert.
Aspect: Verhältnis zwischen Höhe und Breite. 1.0 ist gleiches Verhältnis zwischen Höhe und Breite. Sie sehen aber auch nur dann ein gleiches Verhältnis, wenn auch Ihre Anwendung die gleiche Höhe und Breite hat. Da dies im Vollbildmodus zum Beispiel nicht der Fall ist, können Sie hier zum Beispiel auch Anwendung.Breite/Anwendung.Höhe angeben, um sicherzustellen, dass das Verhältnis immer gleich bleibt.
zn: Ab welcher Tiefe von der Kamera ausgehend Vertices bzw. Dreiecke sichtbar sein sollen.
zf: Ab welcher Tiefe von der Kamera ausgehend Vertices bzw. Dreiecke nicht mehr sichtbar sein sollen.
Hier wird der Sichtwinkel wie anfangs besprochen als Winkelmass angegeben. Beide Befehle beziehen sich auf ein linkshändiges Koordinatensystem (zu erkennen an -LH am Ende des Befehls). Natürlich gibt es auch die äquivalenten Befehle für ein rechtshändiges Koordinatensystem.
Damit hätten wir also das Auge, mit dem wir in unserer 3D-Welt gucken, richtig eingestellt. Nun müssen wir nur noch die Lage und Ausrichtung dieses Auges einstellen. Das geschieht mit folgendem Befehl:
function D3DXMatrixLookAtLH(out mOut: TD3DXMatrix;
var Eye, At, Up : TD3DXVector3) : PD3DXMatrix;
|
MOut: Eine Variable vom Typ D3DXMatrix, die mit den entsprechenden Zahlen gefüllt wird.
Eye: Ein Vektor vom Typ D3DXVECTOR3 oder D3DVECTOR, der die Position des Auges angibt.
At: Ein Vektor vom Typ D3DXVECTOR3, der den Punkt angibt, auf den geguckt wird. Dieser Vektor ist ein absoluter Vektor, also nicht abhängig von Eye. Geben Sie 0/0/0 an, dann wird immer auf den Nullpunkt geguckt, egal wo Sie sich grade befinden. Dies ist vor allem dann sehr hilfreich, wenn Sie eine Kamerabewegung erzeugen wollen, bei der ein fester Punkt immer im Zentrum des Blickfeldes sein soll.
Up: Ein Vektor vom Typ D3DXVector3, der angibt, wo eigentlich 'oben' ist. 0/1/0 ist wohl die gewöhnlichste Einstellung.
Auch zu diesem Befehl gibt es das entsprechende Gegenstück für Rechtshändige Koordinatensystem. Die Funktion lautet D3DXMatrixLookAtRH. In unserem Beispielprogramm wollen wir zunächst aus einer gewissen Höhe und Distanz zum Zylinder auf denselbigen gucken, und zwar mit einer möglichst realistischen Einstellung. Damit dieser Theorieteil nicht zu unübersichtlich wird, finden Sie den Code an 
dieser Stelle. In unserer Anwendung erscheint der Zylinder zum ersten Mal dreidimensional:
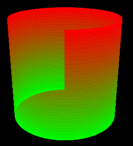
Der grafische Fehler im Bild kommt daher, dass wir noch keinen Z-Buffer verwenden. Zur Zeit rendert DirectX den Zylinder beginnend mit der vordersten Seite im Uhrzeigersinn. Dabei wird auch die hintere Fläche komplett gerendert, da DirectXGraphics noch nicht erkennt, dass die hintere Fläche von der vorderen überlagert wird. Wenn Sie es nicht erwarten können, einen normalen Zylinder zu sehen, dann lesen Sie im Abschnitt Einstellen des Z-Buffers weiter. Ansonsten beschäftigen wir uns in den nächsten 4 Abschnitten mit dem Transformieren von 3D-Körpern.
Translation meint hier im Grunde nichts anderes, als das Bewegen von Vertices im Raum. Im Kapitel Matrizen wird gezeigt, welche Felder der Matrix hier betroffen sind. Obwohl also das Beschreiben der drei Felder sehr einfach ist, gibt es auch hierfür eine Funktion, die das für uns übernimmt. Diese sieht wie folgt aus (MOut wird zukünftigt nicht mehr erklärt. Es handelt sich immer um die Matrix, die mit Zahlen gefüllt wird):
function D3DXMatrixTranslation( out MOut: TD3DXMatrix,
x, y, z: Single): PD3DXMatrix;
|
x,y und z: Die Koordinaten, um die die Vertices bewegt werden sollen.
In diesem Beispielcode finden Sie diese Funktion integriert.
Die Rotation, also das Drehen der Vertices, geschieht immer um den Nullpunkt. Für alle drei Achsen gibt es folgende Funktionen:
function D3DXMatrixRotationX(var mOut : TD3DXMatrix;
const angle : Single) : PD3DXMatrix;
function D3DXMatrixRotationY(var mOut : TD3DXMatrix;
const angle : Single) : PD3DXMatrix;
function D3DXMatrixRotationZ(var mOut : TD3DXMatrix;
const angle : Single) : PD3DXMatrix;
|
Angle ist hierbei das Winkelmass, um das die Vertices gedreht werden sollen. Wenn Sie statt dessen die Vertices um eine Achse drehen wollen, die in irgendeiner Weise diagonal im Raum liegt, dann benutzen Sie dafür folgenden Befehl:
function D3DXMatrixRotationAxis( out mOut: TD3DXMatrix;
VAxis: TD3DVector;
angle: Single): PD3DXMatrix;
|
VAxis ist hierbei ein Vektor vom Typ D3DVECTOR und angle der Winkel um den gedreht wird. Dabei werden die Vertices im Uhrzeigersinn gedreht, betrachtet man den Vektor von der Spitze zum Ursprung.
In diesem Beispielcode finden Sie eine dieser Funktion integriert.
Das Skalieren, also das Vergrössern bzw. Verkleinern, eine Objektes geschieht natürlich auch nur um den Nullpunkt. Dabei wird der Abstand von jedem Vertice zum Nullpunkt mit einem Faktor multipliziert. In dem Kapitel Matrizen wird gezeigt, welche Felder der Matrix hier betroffen sind. Die Funktion, die das Eingeben der Faktoren vereinfacht, sieht so aus:
function D3DXMatrixScaling( out MOut: TD3DXMatrix;
x, y, z: Single): PD3DXMatrix;
|
X, Y und Z sind dabei die Faktoren für den x-, y- und z-Abstand des Vertex zum Nullpunkt.
In diesem Beispielcode finden Sie diese Funktion integriert.
Sie können mit Matrizen auch einen Schatten von Ihrem Modell erzeugen. Dabei werden alle Vertices auf eine Ebene projeziert, in Abhängigkeit von der Lichtquelle. Mit folgender Funktion machen Sie aus einem 3D-Objekt einen Schatten von sich selbst.
function D3DXMatrixShadow( out MOut: TD3DXMatrix;
VLight: TD3DXVECTOR4;
Plane: TD3DXPLANE): PD3DXMatrix;
|
VLight: Ist ein 4-dimensionaler Vektor vom Typ D3DXVECTOR4. X, Y und Z geben die Position der Lichtquelle an. W ist ein Wert zwischen 0.0 und 1.0. 0.0 bedeutet, dass an jeder Stelle im Raum das Licht in die gleiche Richtung verläuft. Das ist bei sehr weit entfernte Objekten, wie der Sonne zum Beispiel, der Fall. 1.0 steht für ein Punktlicht. Je weiter also die Ebene von dem Objekt entfernt ist, desto grösser erscheint der Schatten.
Plane: Gibt die Lage und Ausrichtung der Ebene an, auf die der Schatten projeziert werden soll. Plane ist vom Typ D3DXPLANE.
Für das Erstellen einer Ebene (Plane) gibt es auch hier wieder zwei Funktionen, die uns dabei helfen. Je nach dem, was Ihnen grade günstiger erscheint, können Sie zwischen folgenden Funktionen wählen.
function D3DXPlaneFromPoints( out POut: TD3DXPLANE;
v1, v2, v3: TD3DVECTOR);
|
v1, v2, v3 sind dabei Vektoren vom Typ D3DVECTOR, die 3 Punkte der Ebene markieren. Da 3 Punkte im Raum bekanntermassen immer eine grade Fläche bilden, ist es dadurch möglich, die Lage und Ausrichtung der Ebene zu bestimmen. Die andere mögliche Funktion sieht so aus:
function D3DXPlaneFromPointNormal( out POut: TD3DXPLANE;
VPoint: TD3DVECTOR;
vNormal: TD3DVECTOR);
|
VPoint ist dabei ein Punkt auf der Ebene und vNormal ein Vektor der orthogonal zur Ebene verläuft. Beide sind vom Typ D3DVECTOR. Der Punkt bestimmt sozusagen die ungefähre Lage der Ebene, und der Vektor bestimmt, wie schräg die Ebene ausgerichtet ist.
Bei der Schatten-Transformation werden die Vertices also so transformiert, dass Sie auf der Ebene einen Schatten des ursprünglichen Modells bilden. Um also ein 3D-Objekt mit Schatten zu zeigen, müssen Sie das Objekt zweimal rendern. Einmal in seiner normalen Position, und einmal mit der Schattenmatrix. Desweiteren müssen Sie dafür sorgen, dass das Schattenobjekt eine einheitliche dunkle Farbe erhält, sonst würde es so aussehen, als ob das Objekt einfach nur gegen eine Wand geklatscht ist und zusammengepresst worden ist. In diesem Beispielcode finden Sie die oben vorgestellten Funktion integriert.
Jetzt haben Sie alle grundlegenden Transformationsmethoden kennengelernt. Doch was ist, wenn Sie zum Beispiel mehrere Transformationen miteinander kombinieren wollen? Wenn Sie zum Beispiel wollen, dass sich das Objekt um seine eigene Achse dreht, aber 3 X-Einheiten entfernt von der Ausgangslage? Dann kommt das Multiplizieren von Matrizen mit ins Spiel. Durch multiplizieren zweier Matrizen verbinden Sie die beiden Transformationen aus den Matrizen in einer. Die Funktion dafür sieht so aus:
function D3DXMatrixMultiply( out MOut: TD3DXMATRIX;
M1: TD3DXMATRIX;
M2: TD3DXMATRIX);
|
M1, M2 sind dabei die beiden Matrizen, die miteinander multipliziert werden sollen.
Im Gegensatz zum Multiplizieren von Zahlen, ist es ein Unterschied, in welcher Reihenfolge Sie die Matrizen angeben. Angenommen wir haben die Matrix matMove, die die Vertices einfach nur verschiebt, und eine Matrix matRotationY, die Vertices um die Y-Achse rotieren lässt. Wenn wir nun schreiben würden,
D3DXMatrixMultiply( matResult, matMove, matRotate); |
D3DXMatrixMultiply( matResult, matRotate, matMove); |
Der Z-Buffer ist ein zusätzlicher Speicher, der zu jedem Pixel, dass auf dem Bildschirm gerendert wird, eine Tiefeninformation speichert, im Prinzip also die Distanz von der Kamera zur jeweiligen Stelle des Objektes. Wenn nun ein zweites Objekt gerendert wird, dass unter anderem den gleichen Pixel auf dem Bildschirm beinhalten würde, dann wird geprüft, ob der neue Pixel näher an der Kamera liegt, als der bereits gemalte Pixel. Durch diese Abfragetechnik kann sichergestellt werden, dass Objekte, die sich im Hintergrund befinden nicht Objekte überlagern, die sich im Vordergrund befinden.
An dieser Stelle wird nur kurz beschrieben, wie Sie den Z-Buffer aktivieren. In einem späteren Kapitel werden wir uns näher mit Tiefenbuffern beschäftigen, und wie man die Performance dieser für seine Zwecke optimieren kann.
Damit Sie nach all den vielen Informationen auch endlich Resultate sehen können, hier die notwendigen Schritte, um einen Z-Buffer zu verwenden.
1. Z-Buffer initialisieren:
Wenn Sie Ihr Device initialisieren, übergeben Sie dem unter anderem ein Record namens D3DPRESENT_PARAMETERS. In diesem Record können Sie einstellen, ob Sie einen Tiefenbuffer verwenden möchten, und wenn ja, welches Format er haben soll. Das könnte dann zum Beispiel so aussehen:
var d3dpp : TD3DPRESENT_PARAMETERS; begin ... d3dpp.EnableAutoDepthStencil := TRUE; d3dpp.AutoDepthStencilFormat := D3DFMT_D16; |
2. Z-Buffer aktivieren
Sie müssen dem Device mitteilen, dass es beim Rendern den Z-Buffer auch benutzen soll. Das geht über die Renderstates:
d3ddev8.SetRenderState( D3DRS_ZENABLE, CARDINAL( TRUE ) ); |
3. Z-Buffer regelmässig löschen
Wie auch unser Renderfenster, muss auch der Z-Buffer mit jedem neuen Frame gereinigt werden, dass heisst also, von den alten Tiefenzahlen befreit werden, damit wir das nächste Bild korrekt darstellen können. Dazu bauen wir das entsprechende Flag in die .Clear-Funktion des Devices ein:
d3dDev8.Clear( 0, nil, D3DCLEAR_TARGET or D3DCLEAR_ZBUFFER, D3DCOLOR_XRGB( 50, 50, 50 ), 1.0, 0 ); |
Jetzt ist alles nötige eingestellt, damit es beim Rendern zu keinen optischen Fehlern kommt.
Jetzt ist es mal wieder an der Zeit, sich den mitgelieferten Beispielcode genauer anzuschauen. Sie finden Ihn im directxgraphics/demos/Matrizen und Z-Buffer/-Verzeichnis (Achtung: nur in der Offline-Version). Mit den in diesem Kapitel beschriebenen Transformationsmatrizen und guten Modellen für den Vertexbuffer lässt sich schon eine Menge machen. Der Zylinder ist eher ein mageres Beispiel dafür, was alles durch reine Algorithmik möglich ist.
Zum ersten Mal werden Sie auch eine Animation, also Bewegung im Bild, sehen. Eine Bewegung bzw. Rotation kommt allein dadurch Zustande, dass man von Frame zu Frame die Zahlen für die Matrizen ein wenig ändert. Hierbei helfen wir uns, in dem wir GetTickCount in die Funktionen miteinbinden. GetTickCount liefert uns die aktuelle Zeit in Form einer grossen Zahl zurück. Da sich diese Zahl jede Tausendstelsekunde erhöht, verlangsamen wir das Tempo, in dem wir GetTickCount durch eine 3- oder 4-stellige Zahl teilen. Das langsame Anwachsen dieser Zahl ist geeignet für einen Animationsablauf. Desweiteren bietet sich beim Übernehmen der aktuellen Zeit ein weiterer Vorteil: es wird sichergestellt, dass auf jedem Rechner, egal wie schnell dieser ist, die Bewegung gleich schnell abläuft. Die Anzahl der Frames pro Sekunde hat also auf die Geschwindigkeit der Animation keinen Einfluss. Es ist allein die Zeit.
Hier die einzelnen Codeabschnitte aus den behandelten Kapiteln
procedure SetupViewAndProjection; var matView, matProj: TD3DXMatrix; _v1, _v2, _v3 : TD3DXVector3; begin // View. _v1 := D3DXVector3( 0.0, 2.0, -5.0); _v2 := D3DXVector3( 0.0, 0.0, 0.0); _v3 := D3DXVector3( 0.0, 1.0, 0.0); D3DXMatrixLookAtLH(matView, _v1, _v2, _v3); D3DDEV8.SetTransform(D3DTS_VIEW, matView); // Projection. D3DXMatrixPerspectiveFovLH(matProj, D3DX_PI / 4, form1.width/form1.height, 1.0, 100.0); D3DDEV8.SetTransform(D3DTS_PROJECTION, matProj); end; |
Translation, Rotation, Skalierung
|
procedure Schatten; var matshadow, matWorld: TD3DXMatrix; plane: TD3DXPlane; vlicht: TD3DXVector4; v1, v2, v3: TD3DXVector3; begin v1:= D3DXVector3( -1, -1, 0); v2:= D3DXVector3( 0, -1, 0); v3:= D3DXVector3( -1, -1, -1); D3DXPlaneFromPoints( plane, v1, v2, v3); vlicht:= D3DXVector4(4, 4, 4, 1); D3DXMatrixShadow( matShadow, vlicht, plane); d3ddev8.GetTransform( D3DTS_WORLD, matWorld); D3DXMatrixMultiply( matWorld, matWorld, matShadow); d3ddev8.SetTransform( D3DTS_WORLD, matWorld); end; |
Nehmen Sie sich für das Ausprobieren des Programms ruhig Zeit, und versuchen Sie, die Bewegungen der Körper und der Kamera zu verändern. Wie Sie feststellen werden, lassen sich mit vergleichsweise wenig Veränderungen im Quellcode neue Animationen erzeugen.
Entscheidend hierbei ist die OnIdle-Prozedur, die mit den Prozeduren SetupZylinder1 und SetupZylinder2 die Matrizen für den zu rendernden Zylinder einstellt und mit der Prozedur Schatten eine Matrix für den Schatten des Zylinders erstellt.
Neben den oben genannten Transformationsmöglichkeiten gibt es noch ein paar weitere, die ich Ihnen hier kurz vorstellen möchte.
Determinante
function D3DXMatrixfDeterminant( m: TD3DXMatrix): Single; |
Einheitsmatrix
function D3DXMatrixIdentity(out mOut : TD3DXMatrix) : TD3DXMatrix; |
Kontrolle auf Einheitsmatrix
function D3DXMatrixIsIdentity(const m : TD3DXMatrix) : BOOL; |
Reflektion
function D3DXMatrixReflect( out MOut: TD3DXMatrix; Plane: TD3DXPlane): TD3DXMatrix; |
D3DXPLANE gespiegelt werden.
Vertauschen
function D3DXMatrixTranspose( out MOut: TD3DXMatrix; M: TD3DXMatrix): TD3DXMatrix; |
In den letzten Kapiteln haben Sie gelernt, wie Sie dem Device eine sogenannte Welt-Matrix übergeben. Das Device wendet dabei diese Matrix auf alle Vertices zu 100% an. Was soll man auch anderes erwarten? höre ich Sie jetzt fragen. Ganz einfach. Sie können dem Device noch mehr Weltmatrizen übergeben, und dann selbst bestimmen, zu welchen Anteilen diese Matrizen auf die Vertices angewendet werden. Im Prinzip werden also diese Matrizen miteinander vermischt, was man auch als Überblenden bezeichnen kann.
Um diese Technik nutzen zu können, müssen Sie Ihrem Vertexformat zunächst etwas hinzufügen. Und zwar eine der folgenden Flags aus den D3DFVFFLAGS.
D3DFVF_XYZB1 D3DFVF_XYZB2 D3DFVF_XYZB3 D3DFVF_XYZB4 D3DFVF_XYZB5 |
Wenn Sie die eigentliche Weltmatrix mit einer zweiten Vermischen wollen, dann verwenden Sie das Flag D3DFVF_XYZB1, bei 3 Matrizen, also zwei zusätlichen Matrizen, die ineinandergeblendet werden sollen, verwenden Sie D3DFVF_XYZB2 usw. . Die Blendfaktoren werden direkt nach den Positionskoordinaten angegeben. Das sieht dann bei D3DFVF_XYZB2 so aus:
const
D3DFVF_CUSTOMVERTEX = ( D3DFVF_XYZB1 or D3DFVF_DIFFUSE );
type
CUSTOMVERTEX = record
x, y, z: single;
b1, b2: single;
color: TD3DColor;
end;
|
b1 und b2 liegen dabei zwischen 0.0 und 1.0, wobei 1.0 bedeutet, dass die normale Weltmatrix zu 100% übernommen wird, und 0.0, dass die jeweilige zweite oder dritte Matrix zu 100% übernommen wird. Diese Matrizen übergeben Sie dem Device, in dem Sie in der SetTransform-Funktion D3DWORLD1-D3DWORLD3 aus den D3DTRANSFORMTYPE verwenden. Der letzte Schritt besteht darin, das Matrizenblending über diesen Renderstate einzuschalten:
d3ddev.setrenderstate(D3DRS_VERTEXBLEND, D3DVFB_2WEIGHTS); |
D3DVBF_2WEIGHTS ist dabei eine Konstante aus den D3DVERTEXBLENDFLAGS. Nun werden 3 Matrizen mit den unter b1 und b2 angegebenen Gewichtungen auf die Vertices angewendet.
Zum Schluss möchte ich Ihnen noch etwas zur Projektionsmatrix zeigen. Und zwar haben wir im Kapitel Perspektive und Blickwinkel Matrizen kennengelernt, die uns eine räumliche Vorstellung von Körpern vermitteln können. Was ist aber, wenn wir das gar nicht wollen, sprich, dass Dinge die weiter Hinten, genauso gross dargestellt werden, wie Dinge, die sich weiter vorne befinden. Das ist zum Beispiel bei isometrischen Spielen, wie Age of Empires oder Command&Conquer 3 der Fall. Hier blicken wir von schräg oben auf das Spielfeld und glauben, in die Tiefe zu gucken, je mehr wir uns dem oberen Bildschirmrand nähern. Tatsächlich werden die Felder aber nicht kleiner. Sie bleiben gleich gross. Die untere Montage verdeutlicht den Unterschied an der beiligenden Demo.
Das linke Bild enthält eine orthogonale Projektionsmatrix. Sie erkennen das zum Beispiel daran dass der Durchmesser des rechten Zylinders in die Tiefe hin nicht kleiner wird. Anders ist das im rechten Screenshot. Hier erhalten wir einen realistischen Eindruck räumlicher Tiefe.
Statt der Funktion D3DXMatrixPerspectiveLH() oder D3DXMatrixPerspectiveFovLH() können Sie folgende beiden Funktionen verwenden, um diesen Effekt erzielen zu können.
function D3DXMatrixOrthoLH( out MOut: TD3DXMatrix;
w: Single;
h: Single;
zn: Single;
zf: Single): TD3DXMatrix;
|
w und h geben an, wieviele Welteinheiten in der Vertikalen und Horizontalen dargestellt werden sollen. zn (z-near) und zf (z-far) geben an, ab welcher Tiefe Objekte sichtbar sein sollen, und ab welcher Tiefe nicht mehr.
Mit der zweiten Funktion lassen sich im Prinzip die gleichen Ergebnisse erzielen, wie mit der ersten Funktion. Sie setzt lediglich andere Parameter vorraus.
function D3DXMatrixOrthoOffCenterLH( out MOut: TD3DXMatrix;
l: Single;
r: Single;
b: Single;
t: Single;
zn: Single;
zf: Single): TD3DXMatrix;
|
l und r ist der Bereich auf der x-Achse der angezeigt werden soll. Wenn also der Nullpunkt im Zentrum ihres Bildes sein soll, und Sie alles abbilden möchten, was sich 2 Welteinheiten von diesem Punkt entfernt befindet, so geben Sie hier an -2 und 2.
b und t markieren die sichtbaren Grenzen in der Vertikalen.
zn und zf markieren die sichtbaren Grenzen in der Tiefe.
