Einleitung
Dieses Kapitel klärt lediglich das Grundlegendste an Basiswissen ab bezüglich der Bestandteile der dreidimensionalen Darstellung. Die spezielle Theorie zum Definieren der Vertices, der Funktionsweise der Beleuchtung oder der Art und Weise, wie Texturiert wird, wird in den jeweiligen Kapiteln erläutert, bevor es in die Praxis geht.
Das Koordinatensystem
Die meisten Anwendungen benutzen zwei Arten des kartesischen Koordinatensystems: das linkshändige oder das rechtshändige Koordinatensystem. Beiden gemeinsam ist die Tatsache, dass die x-Achse nach rechts und die y-Achse nach oben verläuft. Um sich die Richtung der z-Achse leichter merken zu können gibt es folgenden Trick: man bewegt die linke oder die rechte Hand so, dass die Finger in die x-Richtung zeigen und die Handinnenfläche nach oben. Die Richtung, in die der Daumen zeigt, ist die Richtung der z-Achse.

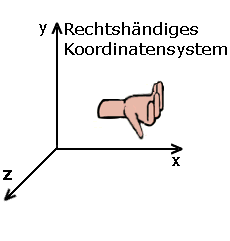
DirectX8.0 nutzt das linkshändige Koordinatensystem. Falls Sie also Anwendungen mit einem rechtshändigen Koordinatensystem nach DirectX übertragen wollen, ist es notwendig, dass Sie bestimmte Änderungen an Ihren 3D-Objekten vornehmen. Darauf werden wir jedoch später noch näher eingehen.
Vektoren
Vektoren sind ein wesentlicher Bestandteil in der Programmierung mit DirectXGraphics. Sie finden in der 3D-Programmierung sehr vielseitige Anwendungsmöglichkeiten. Eine vollständige Erläuterung dieser Thematik würde den Rahmen dieser Dokumentation sprengen, deshalb sei hier nur das nötigste erwähnt. Die Grafik zeigt einen Vektor im zweidimensionalen Raum. Gerichtete Vektoren werden grundsätzlich als Pfeil dargestellt.
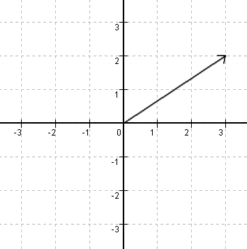
Vektoren geben also eine Richtung an, die in verschiedenen Bereichen der 3D-Programmierung verwendet werden können. Zum Beispiel wird die Position von Vertices über Vektoren definiert. Desweiteren spielen Vektoren im Zusammenhang mit Matrizen eine wichtige Rolle. Im Kapitel  Transformationen und Tiefenbuffer werden wir näher darauf eingehen. Eine konkrete Verwendung finden Vektoren aber zum Beispiel auch in der Einstellung des imaginären Auges, mit dem die 3D-Szene betrachtet wird. Lage und Richtung werden auch hier wieder als Vektoren übergeben.
Transformationen und Tiefenbuffer werden wir näher darauf eingehen. Eine konkrete Verwendung finden Vektoren aber zum Beispiel auch in der Einstellung des imaginären Auges, mit dem die 3D-Szene betrachtet wird. Lage und Richtung werden auch hier wieder als Vektoren übergeben.
Vertices und Dreiecke
Ein Vertex ist ein einzelner Punkt im Raum. Er ist die Grundlage der dreidimensionalen Darstellung. Drei Vertices lassen sich als Dreieck darstellen und aus Dreiecken dreidimensionale Körper. Die Tatsache, dass man alle dreidimensionalen Modelle aus Dreiecken zusammensetzt, beruht auf einer besonders praktischen Eigenschaft von Dreiecken: egal wie man die Punkte im Raum positioniert, das Dreieck hat garantiert immer eine glatte Fläche. Rein theoretisch könnte man mit vier Vertices auch Rechtecke bilden, doch das Füllen dieser Rechtecke mit einer Textur wäre zu zeitintensiv in anbetracht der Tatsache, dass die vier Vertices nicht unbedingt alle auf einer Ebene liegen müssen. Deshalb greift man lieber auf Dreiecke zurück.
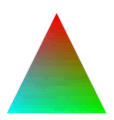
Zunächst verfügt jeder Vertex über seine Positionskoordinaten x, y und z. Doch ein Vertex kann noch über viel mehr Informationen verfügen. Sie können zum Beispiel jedem Vertex einen Farbe zuweisen. Wenn der Vertex nur als Punkt dargestellt wird erscheint der Vertex in seiner jeweiligen Farbe. Wenn der Vertex jedoch in ein Dreieck mit eingebunden ist, wird das Dreieck bis zu einem gewissen Grad, den Sie auch selbst bestimmen können, in die jeweilige Farbe eingefärbt. Das Bild zeigt wie so etwas zum Beispiel aussehen kann. Hier haben die Vertices die Farben Rot, Grün und Türkis. Alle drei Farben haben die gleiche Stärke und sind deshalb zu gleichen Teilen im Dreieck vertreten. Diese Farbgebungen kann man auch dazu benutzen Texturen, die man auf das Dreieck legt, in eine gewünschte Farbe zu tauchen. Sie können zum Beispiel damit auch bestimmte Bereiche dunkler erscheinen lassen, in dem Sie einfach den jeweiligen Ecken eine dunkle Farbe zuweisen. Darüberhinaus können Vertices Koordinaten für mehrere Texturen besitzen und sogenannte Normalvektoren.
Primitiven und Polygone
Eine 3D-Primitive ist eine Menge an Vertices, die ein Objekt bilden. Die einfachste Primitive ist ein einzelner Punkt. Primitiven können aber auch Dreiecke bzw. Dreiecksaneinanderreihungen sein.
Oftmals sind Primitiven auch Polygone. Ein Polygon ist ein geschlossenes 3D-Modell, dass sich aus mindestens 3 Vertices definiert. Hier sehen Sie einen Würfel, ein Polygon bestehend aus 8 Vertices die über Dreiecke miteinander verbunden sind.
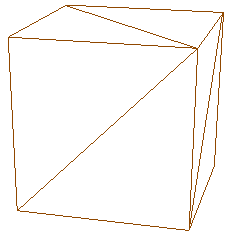
Obwohl Ihnen in DirectXGraphics nur Dreiecke als kleinstes Polygon zur Verfügung stehen, können Sie damit 3D-Körper erzeugen, die rund bzw. gewölbt wirken. Dies hängt allein davon ab, wieviele Dreiecke Sie verwenden.
Normale
Jeder Vertex kann über eine Normale verfügen. Eine Normale ist ein Vektor, der angibt, wie ein Vertex ausgerichtet ist. Dies ist notwendig, wenn Lichtquellen mit ins Spiel kommen. Dann kann anhand der Ausrichtung der Normale zur Lichtquelle ermittelt werden, wie stark ein Vertex bzw. die damit verbundene Fläche angestrahlt wird.
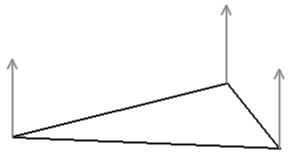
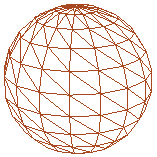
Normalen müssen nicht unbedingt orthogonal zur Fläche verlaufen. Wenn Sie in eine nicht orthogonale Richtung zur Dreiecksfläche zeigen, lassen sich Wölbungen vortäuschen. Die beiden unteren Kugeln demonstrieren den Unterschied.

Die linke Kugel benutzt überhaupt keine Normal-Vektoren. DirectXGraphics rendert daher jede Fläche mit einer ganzheitlichen Schattierung. Unter geschickter Benutzung von Normal-Vektoren kann man jedoch diese Schattierung interpolieren lassen, so dass man den Eindruck erhält, die Fläche wäre gewölbt.
Reihenfolge, in der Vertices definiert werden
Bei Dreiecken wird für gewöhnlich unterschieden zwischen einer Vorder- und einer Rückseite. Die Vorderseite eines Dreiecks wird gerendert, die Rückseite nicht. Als Vorderseite gilt standardmässig die Seite, bei der die Vertices im Uhrzeigersinn angeordnet sind. Grundsätzlich können Sie aber in DirectXGraphics auch einstellen, dass Dreiecke, bei denen die Vertices gegen den Uhrzeigersinn angeordnet sind, gerendert werden sollen oder das beide Seiten in jedem Fall gerendert werden sollen. Das Nicht-Rendern einer Dreiecksseite aufgrund der Vertex-Anordnung bezeichnet man als Culling.
Wie Vertices zu Primitiven werden
Um 3D-Modelle von Hand zu erstellen, können Sie Vertices auf 6 verschieden Arten miteinander verbinden.
Punktliste (Point List)
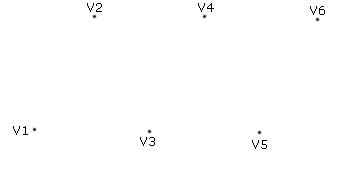
Jeder Vertex wird als Punkt gerendert und stellt damit eine einzelne Primitive dar.
Linienliste (Line List)
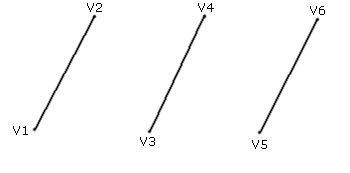
Jeder Vertex wird mit dem nachfolgenden verbunden. Danach wird mit dem nächsten Vertex wieder eine neue Linie begonnen.
Linienkette (Line Strip)
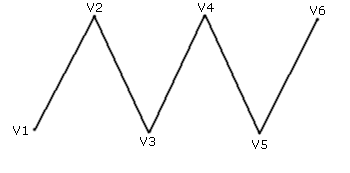
Alle Vertices werden der Reihe nach miteinander verbunden.
Dreiecksliste (Triangle List)
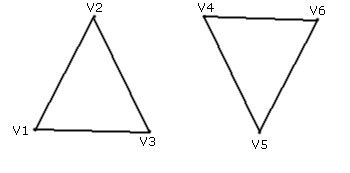
Jeweils drei aufeinanderfolgende Vertices werden zu einem Dreieck verbunden. Mit dem nächsten Vertex wird wieder ein neues Dreieck begonnen. Diese Technik eignet sich für die meisten 3D-Modelle, wenn folgende Technik nicht funktioniert.
Dreieckskette (Triangle Strip)
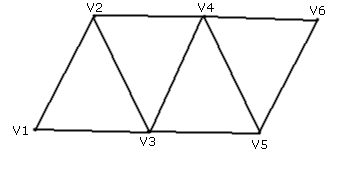
Die ersten 3 Vertices werden zu einem Dreieck verbunden, jedes folgende Vertex wird mit den letzten beiden Vertices verbunden. So bilden V1, V2, V3 ein Dreieck, V2, V3, V4 ein Dreieck usw. Dies ist die effizienteste Art Dreiecke zu Rendern und damit 3D-Modelle zu erstellen. Je nach Geometrie jedoch nicht immer anwendbar.
Dreiecksfächer (Triangle Fan)
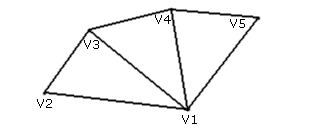
Hierbei werden V1, V2, V3 zu einem Dreieck verbunden, danach V1, V3, V4 usw.. Diese Technik ist vorallem bei kegelartigen Objekten sehr sinnvoll.
 SelfDXD ---
SelfDXD ---
 DirectX Graphics ---
DirectX Graphics ---  Theoretisches Vorwissen
Theoretisches Vorwissen


 Einleitung
Einleitung Das Koordinatensystem
Das Koordinatensystem Vektoren
Vektoren Vertices und Dreiecke
Vertices und Dreiecke Primitiven und Polygone
Primitiven und Polygone Normale
Normale Reihenfolge, in der Vertices definiert werden
Reihenfolge, in der Vertices definiert werden Wie Vertices zu Primitiven werden
Wie Vertices zu Primitiven werden














