SelfDXD --- DirectX Graphics --- Theoretisches Vorwissen
	Berechnung von Rotationen
	Einleitung Sinus, Cosinus und der Einheitskreis Rotieren in 2D Rotieren in 3D

Wenn Sie mit der Programmierung einer dreidimensionalen Anwendung beginnen, werden Sie feststellen, dass das Rotieren von Objekten ein sehr wichtiges Element in der Erstellung von Animationen sein kann. In diesem Kapitel geht es um die reine Mathematik, die hinter dem Rotieren von Punkten um eine Achse steht. Das Kapitel wendet sich an alle, die in der Schule dieses Thema, aus welchen Gründen auch immer, versäumt haben.

Dieses Kapitel erklärt die Materie in einem zweidimensionalen Koordinatensystem. Doch alle hier erwähnten Dinge lassen sich problemlos in die dritte Dimension übertragen.

Ja da war doch irgendwas, höre ich Sie jetzt sagen! In der Tat, Sinus und Cosinus haben irgendwas mit einem Einheitskreis zu tun. Ein Einheitskreis ist ein Kreis mit dem Radius 1. Das heisst die Strecke vom Mittelpunkt des Kreises zum Rand ist genau eine Längeneinheit lang. Wenn wir nun einen Punkt haben, den wir von den Koordinaten (1, 0), also dem rechtesten Punkt im Einheitskreis, aus um einen bestimmten Winkel a verschieben wollen, dann liefert uns cos(a) die x-Koordinate des Punktes auf dem Einheitskreis und sin(a) die y-Koordinate.

Wenn wir den Punkt also zum Beispiel um 90° bewegen, erhalten wir: cos(90) = 0 und sin(90) = 1. Die Koordinaten unseres Punktes wären demzufolge dann also (0, 1).

Nun kommt beim Rechnen mit Winkelfunktionen mit dem Computer noch eine Besonderheit hinzu. Der Computer erwartet als Eingabe für sin() und cos() keinen Winkel sondern ein Bogenmass, also den Umfang des Kreisabschnittes. Der Umfang des Einheitskreises beträgt 2*Pi. Pi ist eine Zahl mit unendlich vielen Stellen nach dem Komma (Pi = 3,1415926535897932384626433832795...). Für das Arbeiten am Computer reichen jedoch für eine hohe Genauigkeit die ersten 9-13 Stellen.

Um also aus dem Winkel das Bogenmass zu erhalten rechnen wir: Winkel / 180 * PI
In der unteren Grafik ist a_B demzufolge das Bogenmass, bei dem die selben Koordinaten herauskommen, wie beim oberen Beispiel die Eingabe des Winkels a.

Um also einen Punkt, oder im Spiel ein ganzes Objekt um eine Achse rotieren zu lassen, müssen Sie lediglich kontinuirlich den Winkel verändern um den der Punkt von seiner Ausgangslage aus gedreht werden soll. Angenommen Sie haben nun einen Punkt, der r Einheiten von der Achse entfernt um diese kreisen soll. Da wir bei Berechnungen mit Sinus und Cosinus immer von einem Einheitskreis ausgehen, bei dem der Radius also 1 beträgt, muessen wir die Ergebnisse, die wir mit sin() und cos() erhalten lediglich mit r multiplizieren, um den Radius auf r zu erhöhen.

Ein Beispiel: Der Punkt soll in einem Abstand von 5 Einheiten um den Nullpunkt gedreht werden. Der gewünschte Winkel ist 40° Grad. Und so sieht die Rechnung dazu aus:

  radWinkel:= 40 / 180 * Pi;            // radWinkel = 0.698131...
  x_koordinate:= cos( radWinkel ) * 5;  // x_koordinate = 3,830222...
  y_koordinate:= sin( radWinkel ) * 5;  // y_koordinate = 3,213938...

Und damit kennen wir die neuen Koordinaten, an denen wir unseren Punkt oder unser 3D-Objekt postieren müssen.

Wenn Sie in einem dreidimensionalen Raum einen Punkt rotieren lassen möchten, dann gibt es im Prinzip zwei Arten von Rotationsberechnungen. Zum einen die Rotationen, bei denen sich nur zwei Koordinaten verändern (also zum Beispiel nur x und y oder x und z oder y und z) und zum anderen die Rotationen, bei denen sich alle drei Koordinaten verändern. Wenn sich nur zwei Koordinaten verändern, dann lässt sich das Problem auf 2D-Ebene lösen. Dann hilft Ihnen der obere Abschnitt weiter. Hier soll es um Rotationen gehen, die (umgangssprachlich gesagt) schräg im Raum stattfinden, in etwa so, wie es der folgende Screenshot zu verdeutlichen versucht.

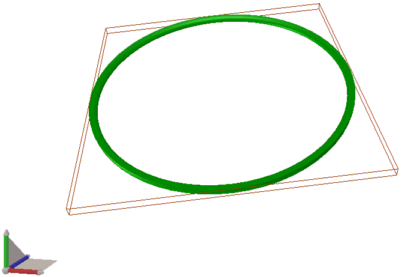
Der Rahmen um die Rotationskurve soll zeigen, dass hier sowohl die Breite wie die Höhe als auch die Tiefe eine Rolle spielen. Wir müssen also die x-, y und z-Koordinaten berechnen, da sich alle drei Koordinaten je nach gewünschtem Winkel verändern.

Die Lösung für dieses Problem ist im Prinzip ganz einfach. Sie berechnen die Rotation zunächst nur auf zweidimensionaler Ebene, beziehen also zum Beispiel nur die x- und z-Koordinate mit ein. Damit zieht Ihr Objekt, dass Sie drehen lassen wollen, einen Kreis, der nur zwei Ebenen verwendet. Wenn Sie also den Kreis noch ein wenig anwinkeln wollen, wie es die obere Darstellung andeutet, muessen Sie jede Koordinate jeweils nochmals um ihre Achse drehen lassen, diesmal aber in Einbeziehung der y-Achse.