 1. Einführung - Szenario
1. Einführung - Szenario
Dank seiner Ausstattung mit zehn Fingern ist für den Menschen der Umgang mit dem
Dezimalsystem die natürlichste Sache der Welt. Man geht davon aus, dass unsere Vorfahren
vor etwa 5000 Jahren begannen, die Dinge, die sie umgaben, zu zählen. Um so schwerer
fällt uns naturgemäß der Umgang mit Zahlensystemen, die nicht auf der Basis 10 beruhen,
etwa dem Dualsystem oder dem Hexadezimalsystem.
In diesem Projekt geht es daher um die Aufstellung und Programmierung von Algorithmen
zur Wandlung des dezimalen Positionssystems in andere Positionssysteme und umgekehrt.
Vorauszusetzendes:
Die Schüler kennen die algorithmischen Grundstrukturen Sequenz, Alternative und Zyklus
und sind in der Lage, diese zur Lösung einfacher Problemstellungen miteinander zu
kombinieren bzw. zu verschachteln.
Kenntnisse zum Datentyp Zeichenkette sowie Fertigkeiten bezüglich Zugriff und
Manipulation einzelner Elemente der Kette werden vorausgesetzt.
Projektverlauf:
Zunächst wird die Überführung einer Dezimalzahl in eine Dualzahl und umgekehrt an
einfachen Beispielen verdeutlicht. Es werden Algorithmen in Struktogrammform abgeleitet
und diese wiederum in eine einfache Oberfläche implementiert.
Anschließend werden die Kenntnisse auf das Problem der Hexadezimalzahlen übertragen und
Lösungen zur Behandlung der Hexadezimalziffern > 9 diskutiert.
Schließlich können die Algorithmen des Projektes soweit verallgemeinert werden, dass die
Basis selbst zur Variablen wird.
 Seitenanfang
Seitenanfang
 2. Aufgabenstellung
2. Aufgabenstellung
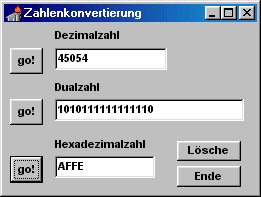 Ähnlich der
Abbildung ist ein Zahlenkonverter zu programmieren, wobei jedes Textfeld zur Eingabe einer
Zahl des angegebenen Zahlensystems genutzt werden kann und auf Betätigung des jeweiligen
Go!-Buttons hin die Wandlung in die beiden verbleibenden Systeme erfolgen soll. Ähnlich der
Abbildung ist ein Zahlenkonverter zu programmieren, wobei jedes Textfeld zur Eingabe einer
Zahl des angegebenen Zahlensystems genutzt werden kann und auf Betätigung des jeweiligen
Go!-Buttons hin die Wandlung in die beiden verbleibenden Systeme erfolgen soll.Für
alle Eingaben ist abzusichern, dass keine "unerlaubten" Zeichen zur Verarbeitung
gelangen.
Empfohlene Vorgehensweise:
- Dezimales und duales Positionssystem
klarmachen!
- Algorithmus "Dezimal in Dual" an Zahlenbeispielen sowie im
Struktogramm nachvollziehen und danach in die Programmoberfläche (vgl. Abb.)
implementieren!
- Besonderheiten des Hexadezimalsystems herausarbeiten, den
Algorithmus "Dezimal in Dual" zu "Dezimal in Hexadezimal" erweitern
und implementieren (in die gleiche Prozedur wie 2.)!
- Programierung der Wandlung "Dual nach Dezimal" -
dabei eine Eingabeprüfung auf korrekte Dualzahl
einarbeiten! Die Konvertierung "Dual in Hexadezimal" kann, nachdem die
entsprechende Dezimalzahl im oberen Edit-Feld ausgegeben wurde, durch Auslösen des
Button1.Click-Ereignisses simuliert werden ;-)
- Die Verfahrensweise von 4. ist auf "Hexadezimal in Dezimal" bzw.
"Hexadezimal in Dual" zu übertragen!
Weiterführende Aufgaben:
- Entwicklung eines Zahlenkonverters, der eine einzugebende Zahl beliebiger Basis (2 <=
Basis <= 36) in ein Ausgabesystem mit ebenfalls beliebiger Basis wandelt. Der
Ziffernvorrat betrage dabei {0...9; A...Z}
- Erweiterung des obigen Konverters für ganze Zahlen auf den Bereich der reellen Zahlen.
(Eine Aufgabe für Freaks, denn hier kapituliert sogar der Windows-Taschenrechner! Wer's
geschafft hat bitte Mail + Attachement an mich
;-)
- Für die Wandlung von Römischen Zahlen in Dezimalzahlen und umgekehrt ist ein Programm
zu entwickeln.
|
 Seitenanfang
Seitenanfang
3. Algorithmisch-programmiertechnische
Grundlagen
|
 3.1. Wandlung Dual in Dezimal
3.1. Wandlung Dual in Dezimal
Machen wir uns zunächst nochmals das Dezimalsystem
(dezimales Positionssystem) klar.
Basis = 10, Ziffern = {0...9}
Beispiel: 1472
| 103 |
102 |
101 |
100 |
|
| 1 |
4 |
7 |
2 |
| = |
2*100 |
+ 7*101 |
+ 4*102 |
+ 1* 103 |
| = |
2*1 |
+ 7*10 |
+ 4*100 |
+ 1*1000 |
| = |
2 |
+ 70 |
+ 400 |
+ 1000 |
| = |
1472 |
|
Diese formale Betrachtungsweise wird auf das Dualsystem übertragen.
Basis = 2, Ziffern = {0; 1}
Beispiel: 11012
| 23 |
22 |
21 |
20 |
|
| 1 |
1 |
0 |
12 |
| = |
1*20 |
+ 0*21 |
+ 1*22 |
+ 1* 23 |
| = |
1*1 |
+ 0*2 |
+ 1*4 |
+ 1*8 |
| = |
1 |
+ 0 |
+ 4 |
+ 8 |
| = |
1310 |
|
Ein entsprechender Algorithmus muss also die Zeichenkette, welche die Dualzahl
präsentiert, vom letzten bis zum ersten Zeichen durchlaufen und jeweils den Zahlwert der
betreffenden Ziffer bilden. (bei Dualzahlen 0 oder 1)
Diese Zahlwerte sind mit den Faktoren der zugehörigen Position zu multiplizieren und zur
Dezimalzahl aufzusummieren. (Verdeutlicht wird dieses Vorgehen an der oben grün
dargestellten Zeile)
Struktogramm Dual in Dezimal
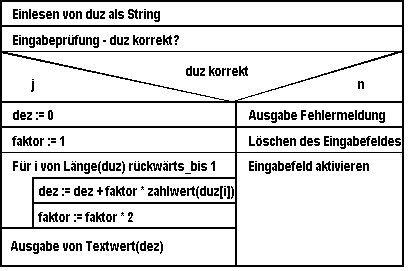
Realisierung der Eingabeprüfung
Es wird für jedes Zeichen überprüft, ob es sich in der erlaubten Wertemenge
befindet. Sollte dies auch nur einmal nicht der Fall sein, ist die Eingabe nicht korrekt.
Hilfreich erweist sich in diesem Fall die Verwendung einer boolschen Variablen.
...;
{Eingabeprüfung}
korrekt := true;
for i := 1 to Length(duz) do
if not (duz[i] in [0..1]) then
korrekt := false;
{Wandlung bei korrekter Eingabe}
if korrekt then
begin
...
end
{Fehlermeldung bei nicht korrekter Eingabe}
else
begin
...
end; |
 Seitenanfang
Seitenanfang
 3.2. Wandlung Dezimal in Dual
3.2. Wandlung Dezimal in Dual
Algorithmus:
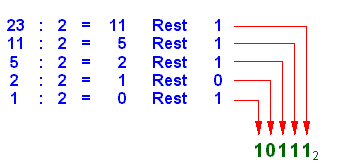 Die Dezimalzahl
wird fortlaufend ganzzahlig mit 2 dividiert. Die Dezimalzahl
wird fortlaufend ganzzahlig mit 2 dividiert.
Der jeweils entstehende Rest wird von rechts nach links an die Dualzahl angefügt.
Das Verfahren endet, wenn das Ergebnis der ganzzahligen Division 0 beträgt. |
| Abb. Wandlung der Dezimalzahl 23 in eine Dualzahl |
Struktogramm Dezimal in Dual

 Seitenanfang
Seitenanfang
 3.3. Besonderheiten des
Hexadezimalsystems
3.3. Besonderheiten des
Hexadezimalsystems
Da dieses Zahlensystem auf der Basis 16 beruht, sind
also auch 16 verschiedene Ziffernzeichen notwendig. Neben den
bekannten Ziffernzeichen 0..9 kommen zusätzlich die Buchstaben A..F als
"Ziffern" zum Einsatz. (siehe Tabelle)
| Dez. |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
... |
| Hex. |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
A |
B |
C |
D |
E |
F |
10 |
11 |
... |
Wandlung Hexadezimal in Dezimal
(Zahlenbeispiel):
| 162 |
161 |
160 |
|
| 2 |
E |
A16 |
| = |
10*160 |
+ 14*161 |
+ 2*162 |
| = |
10*1 |
+14*16 |
+ 2*256 |
| = |
10 |
+ 224 |
+ 512 |
| = |
74610 |
|
Wandlung Dezimal in Hexadezimal
(Zahlenbeispiel):
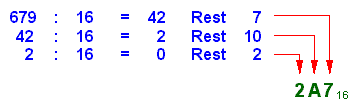 Zu beachten ist dabei, dass für Rest-Werte zwischen 10 und 15 die
entsprechenden Buchstaben eingesetzt werden müssen. Zu beachten ist dabei, dass für Rest-Werte zwischen 10 und 15 die
entsprechenden Buchstaben eingesetzt werden müssen. |
Im Programm kann dies auf verschiedene Weise realisiert werden:
- mit einer geschachtelten IF-THEN-ELSE-Struktur :-(
- mittels CASE-Anweisung :-)
- durch Zugriffe auf die ASCII-Tabelle - siehe Chr(x) / Ord(z) :-)
- unter Verwendung einer Zeichenkettenkonstante, die alle Hexziffern in gegebener
Reihenfolge enthält, wobei der Restwert als Index für die jeweilige Hexziffer fungiert :-))
|
 Seitenanfang
Seitenanfang
 3.4. Spezielle Pascal-Sprachelemente zum Projekt
3.4. Spezielle Pascal-Sprachelemente zum Projekt
| Befehlswort |
Erläuterungen und Beispiele |
| DIV |
Ganzzahlige Division (Weglassen der Kommastellen)
z.B. 7 div 2 => 3 |
| MOD |
Restwert der ganzzahligen Division
z.B. 7 mod 2 => 1 (denn 7 : 2 = 3, Rest 1) |
| Longint |
Datentyp für lange Integer-Zahlen (32 Bit)
Wertebereich (-2147483648 .. 2147483647) |
| IN |
Feststellen einer Mengenzugehörigkeit
z.B. if zeichen in ['0'..'9'] stellt fest, ob der Wert von Zeichen innerhalb der
Zeichenmenge von 0 bis 9 ist.
if buchst in ['a'..'z', 'A'..'Z'] ermittelt, ob buchst mit einem Buchstaben belegt ist |
| Chr(x) |
x ist ein Integer-Ausdruck. Das Ergebnis der Funktion
ist ein Zeichen, dessen ASCII-Code dem Wert von x entspricht. Für x sind Werte von 0 bis
255 zugelassen.z.B. chr(68) => 'D' |
| Ord(z) |
z ist ein ASCII-Zeichen. Das Ergebnis der Funktion ist
derjenige Integer-Wert, der die Position des Zeichens in der ASCII-Tabelle angebt. z.B.
ord('G') => 71 |




 Ähnlich der
Abbildung ist ein Zahlenkonverter zu programmieren, wobei jedes Textfeld zur Eingabe einer
Zahl des angegebenen Zahlensystems genutzt werden kann und auf Betätigung des jeweiligen
Go!-Buttons hin die Wandlung in die beiden verbleibenden Systeme erfolgen soll.
Ähnlich der
Abbildung ist ein Zahlenkonverter zu programmieren, wobei jedes Textfeld zur Eingabe einer
Zahl des angegebenen Zahlensystems genutzt werden kann und auf Betätigung des jeweiligen
Go!-Buttons hin die Wandlung in die beiden verbleibenden Systeme erfolgen soll.
 Die Dezimalzahl
wird fortlaufend ganzzahlig mit 2 dividiert.
Die Dezimalzahl
wird fortlaufend ganzzahlig mit 2 dividiert.
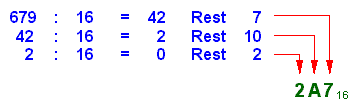 Zu beachten ist dabei, dass für Rest-Werte zwischen 10 und 15 die
entsprechenden Buchstaben eingesetzt werden müssen.
Zu beachten ist dabei, dass für Rest-Werte zwischen 10 und 15 die
entsprechenden Buchstaben eingesetzt werden müssen.