Wasserstein Eigendistances
Wasserstein eigendistances are intrinsic distances of a Markov chain. Here I considered simple random walks on various finite graphs. The distance between two vertices is a measure for how easy it is for the random walk to distinguish the two vertices.
Simulations
The simulations show convergence to Wasserstein eigendistances starting from the trivial distance, where any two distinct nodes have distance 1. That is, we consider the map $$W(\rho)(x,y) = \inf_{\pi_{xy}}\int \rho \;d\pi,$$ where \(\pi_{xy}\) is a coupling of \(P_x\) and \(P_y\), the transition kernel of the random walk when starting in \(x\) or \(y\). Then we let \(\rho_0(x,y)=\delta_x(y)\) and \(\rho_{n+1}=\frac{W(\rho_n)}{\sup_{x,y}W(\rho_n)(x,y)}\). The numerical solutions are then embedded in the plane so that distances across an edge \(xy\) are close to \(\rho_n(x,y)\). The number of iterations increases in each time step to better illustrate the convergence.
6x6 grid
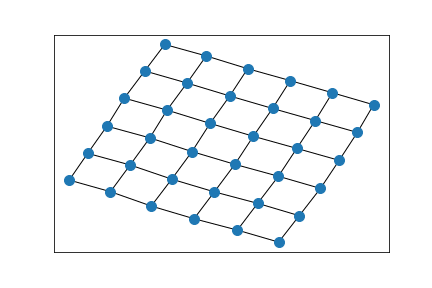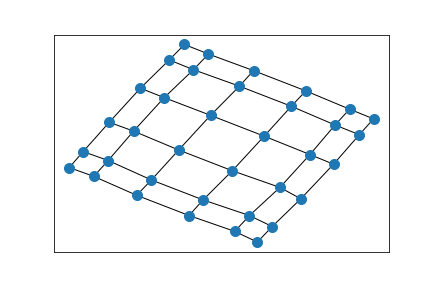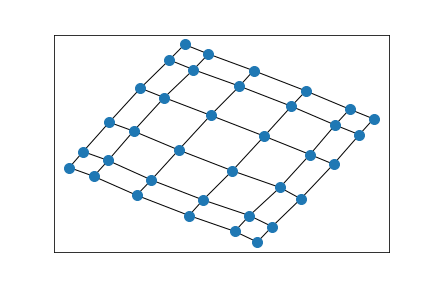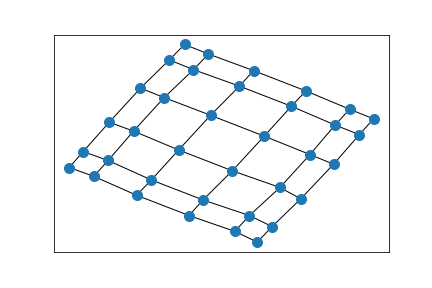
6x4 grid
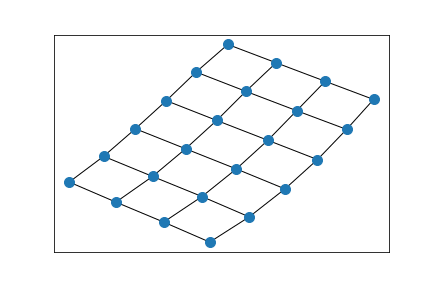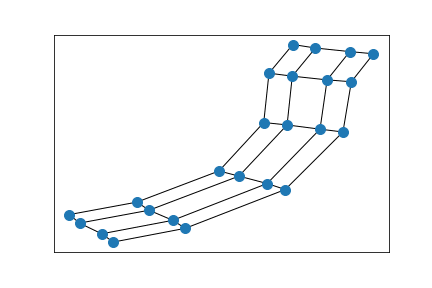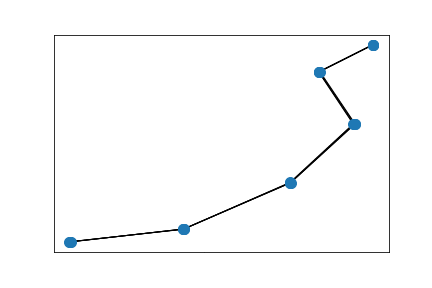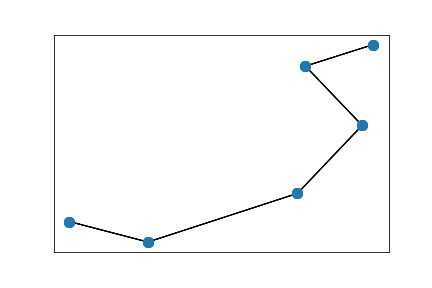
Two connected 5x5 grids
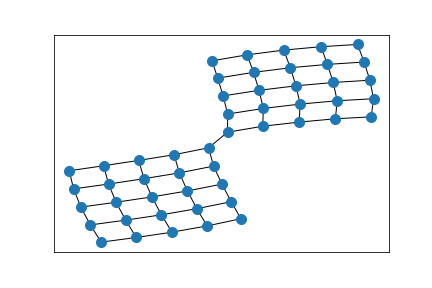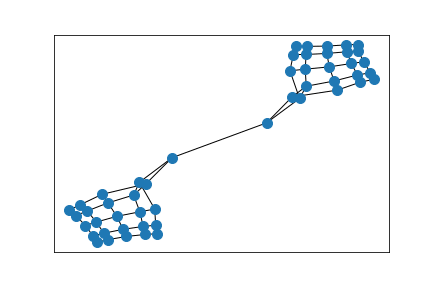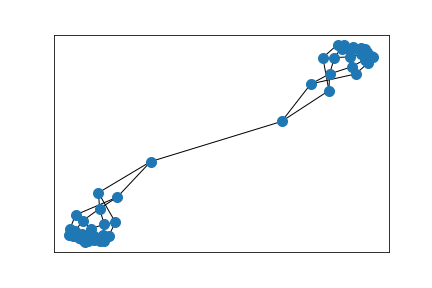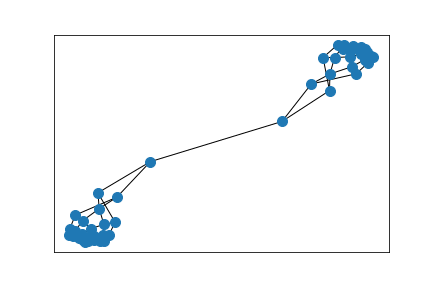
Erdős–Rényi random graph
Another Erdős–Rényi random graph
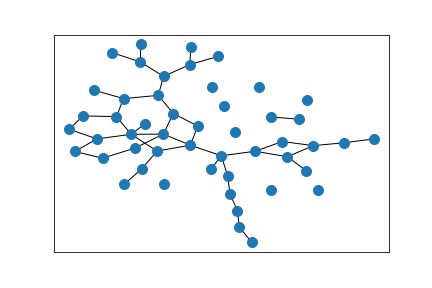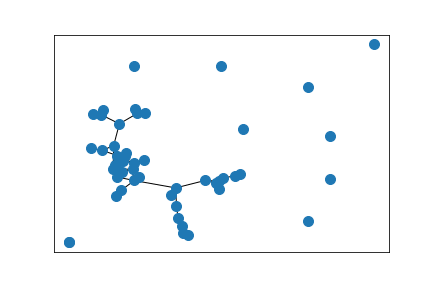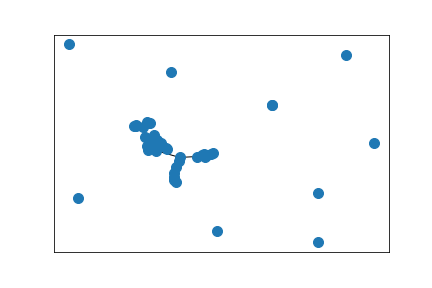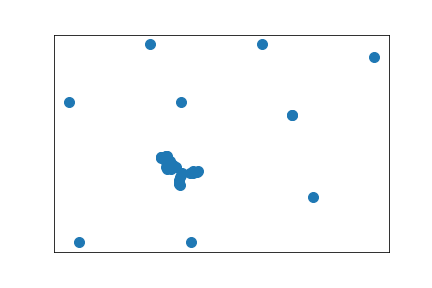
Largest component of above graph
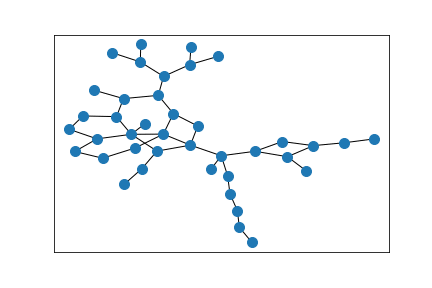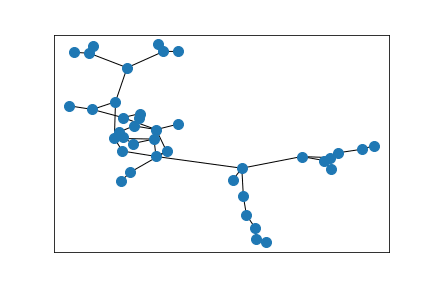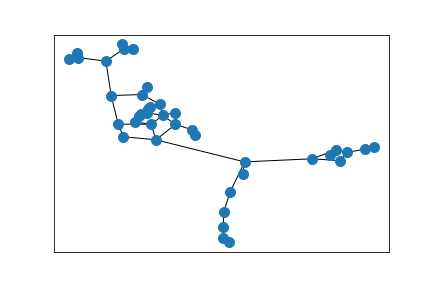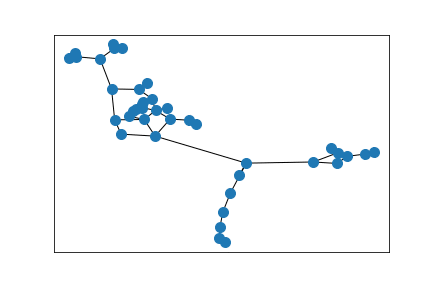
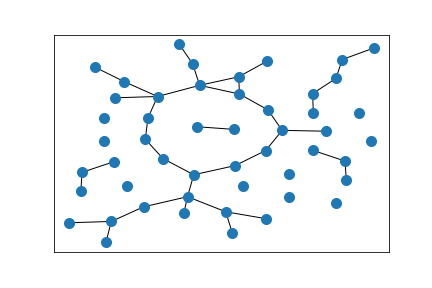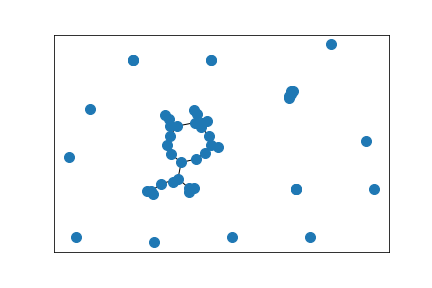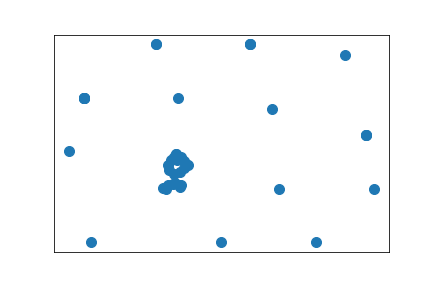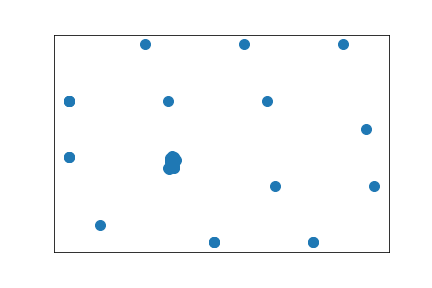
A ring of Erdős–Rényi random graphs
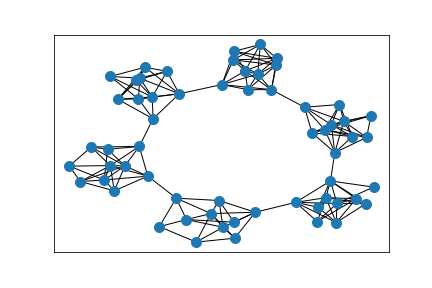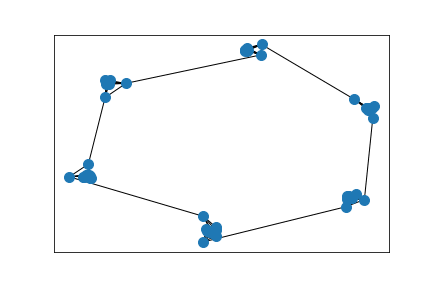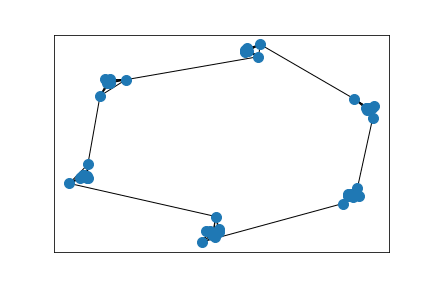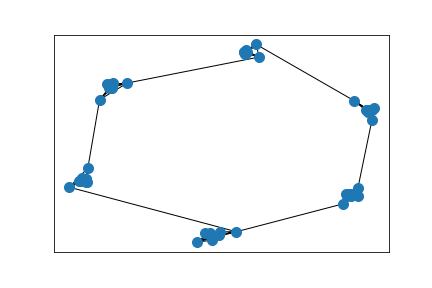
Cluster detection
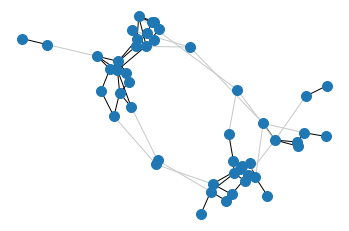
The initial graph, embedded according to graph distance
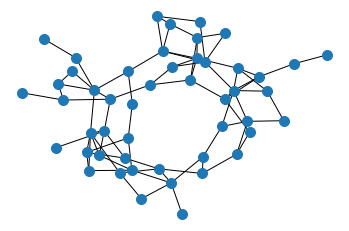
Clustering based on Wasserstein eigendistances across edges less than 0.1
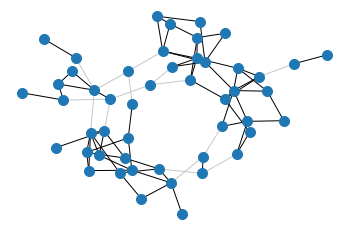
Same, but embedding corresponding to Wasserstein eigendistance