Dr.Quapp: Statistik für Mathematiker mit SPSS
12. Übung - Regression mit Konfidenzintervallen und
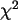 -Anpassung -
-Anpassung -
- 1.
- Der "Schiefe Turm" von Pisa wurde im Dezember 2001 nach langer
Behandlung wieder für Besucher freigegeben. Folgende Meßreihe
schildert das dramatische Vorgeschehen. Angegeben ist die Schiefe
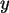 in
Addition zu 2,90
in
Addition zu 2,90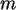 in
in 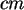 .
. 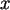 sind die Jahreszahlen.
sind die Jahreszahlen.
| x |
75 |
76 |
77 |
78 |
79 |
80 |
81 |
82 |
83 |
84 |
85 |
86 |
87 |
| y |
6,42 |
6,44 |
6,56 |
6,67 |
6,73 |
6,88 |
6,96 |
6,98 |
7,13 |
7,17 |
7,25 |
7,42 |
7,57 |
(a) Finden Sie die Regressionsgrade. Welcher prozentuale Anteil der
Änderung der Meßwerte ist durch die Gerade erklärbar?
(b) Geben Sie ein 98% Konfidenzintervall CI für den wahren
Anstieg 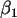 an! Interpretieren Sie dieses Intervall.
an! Interpretieren Sie dieses Intervall.
(c) Die mit dem Problem des "Schiefen Turms" befaßten Bauleute
waren 1987 naturgemäß an einer Aussage interessiert, um wie viele
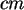 sich der Turm bis z.B. 1997 weiter neigen würde, wenn keinerlei
Korrekturen am Bau vorgenommen werden würden. Nutzen Sie die
Regressionsgerade für eine derartige Vorhersage.
sich der Turm bis z.B. 1997 weiter neigen würde, wenn keinerlei
Korrekturen am Bau vorgenommen werden würden. Nutzen Sie die
Regressionsgerade für eine derartige Vorhersage.
(d) Bestimmen Sie die Fehlergrenze für die vorhersagbare mittlere
Entwicklung der Schiefe im Jahr 1997 für ein 95% CI.
- 2.
- (a) Erzeugen Sie die
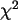 -Verteilung mit 4
Freiheitsgraden:
Zeichnen Sie die Dichte der theoretischen
-Verteilung mit 4
Freiheitsgraden:
Zeichnen Sie die Dichte der theoretischen 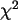 Verteilung
über einer Achse.
Verteilung
über einer Achse.
(b) Bei der Untersuchung über den Schädlingsbefall von Apfelbäumen wurden
drei verschiedene Apfelesorten (A,B,C) überprüft.
Es wurden insgesamt 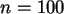 Bäume untersucht. Es ergab sich folgende Kontingenztafel:
Bäume untersucht. Es ergab sich folgende Kontingenztafel:
Man prüfe die Unabhängigkeit von Schädlingsbefall und Sorte
mit einem geeigneten Testverfahren zum Niveau 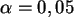 .
.
- 3.
- (a)
Erzeugen Sie die
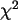 -Verteilung mit 5
Freiheitsgraden:
Zeichnen Sie die Dichte der theoretischen
-Verteilung mit 5
Freiheitsgraden:
Zeichnen Sie die Dichte der theoretischen 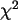 Verteilung
über einer Achse.
Verteilung
über einer Achse.
(b) Erzeugen Sie für das Merkmal X 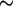 Würfel
je 600 Zufallszahlen.
(Anleitung: Gleichverteilung im Intervall (1.0,6.999) auf ganze Zahlen
reduzieren.)
Würfel
je 600 Zufallszahlen.
(Anleitung: Gleichverteilung im Intervall (1.0,6.999) auf ganze Zahlen
reduzieren.)
Zeichnen Sie ein Histogramm für die sechs Kategorien von X, und
überprüfen Sie die Gleichheit der Ausprägungen der
einzelnen Augenzahlen mit dem 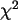 -Anpassungstest.
-Anpassungstest.
Dr.Wolfgang Quapp
2004-12-17
![]() -Anpassung -
-Anpassung -