- Freitag, 15
http://www.mathematik.uni-leipzig.de/MI/quapp/uebungSPSS.html
Hinweise zur 10. Übung No.3 - Stichproben -
3] Es wurden 10 Stichproben eines Glyzerin-Wasser-Gemisches
gezogen. Es ergaben sich folgende Dichten (in g/cm![]() ):
):
1,0768,
1,0772,
1,0766,
1,0765,
1,0774,
1,0771,
1,0775,
1,0770,
1,0769,
1,0770.
Es ist zu prüfen, ob das Gemisch aus 30% Glyzerin besteht, für das
die mittlere Dichete mit ![]() =1,0771 angegeben wird.
=1,0771 angegeben wird.
Das Beispiel ist so klein, daß die Betrachtung auch per Hand
gerechnet werden kann! Um zu prüfen, ob das Gemisch aus 30% Glyzerin
besteht, ist zu testen, ob die mittlere Dichte ![]() gleich der
Dichte
gleich der
Dichte ![]() =1,0771 bei 13
=1,0771 bei 13![]() C ist. Bei der Annahme, das die
gemessenen
C ist. Bei der Annahme, das die
gemessenen ![]() ,...,
,..., ![]() aus einer normalverteilten
Grundgesamtheit stammen, was man bei Messungen immer annimmt, kann der
aus einer normalverteilten
Grundgesamtheit stammen, was man bei Messungen immer annimmt, kann der
![]() -Test angewendet werden.
-Test angewendet werden.
- Hypothese H: ![]() =1,0771
=1,0771
- Kritischer Bereich: Die Testgröße ![]() ist außerhalb
ist außerhalb
![]()
- Entscheidung: Es ist der Mittelwert der 10 Stichproben
![]() =
=
![]() =1.0770
=1.0770
Die empirische Varianz ist
![\begin{displaymath}
s^2 = \frac{1}{9} \ [ \ \sum_{i=1}^{10} (\rho_i - \bar \rho)^2 ] = 1/9 *
0.000\,000\,92 ,
\end{displaymath}](img12.gif)
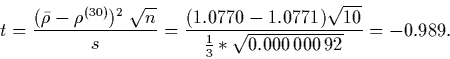
In SPSS hat man die 10 Stichproben als Spalte einzugeben ( oder von D: die Datei glyzerin.sav laden ). Führt man eine explorative Analyse durch, so bekommt man die 95% CI für den Mittelwert zu (1.0768; 1.0772). Da der gefragte Mittelwert 1.0771 enthalten ist, kann man wieder wie in Aufgabe 2) vermuten, daß gegen die Hypothese nichts einzuwenden ist.
Wenn man noch in Betracht zieht, daß auch die Varianz unbekannt ist,
so ist der ![]() -Test zu verwenden.
Mit obigen Daten ist der
-Test zu verwenden.
Mit obigen Daten ist der ![]() -Test für "eine"
durchgehende Stichprobe aufzurufen.
In einem Fenster ist hier der Testwert des Mittelwertes 1.0771 noch
einzugeben.
Es ergibt sich der oben schon berechnete
-Test für "eine"
durchgehende Stichprobe aufzurufen.
In einem Fenster ist hier der Testwert des Mittelwertes 1.0771 noch
einzugeben.
Es ergibt sich der oben schon berechnete ![]() -Wert -0.989 und die 2-seitige
Signifikanz von 0.348 ist weit größer als das erforderliche Kriterium
0.05 .
-Wert -0.989 und die 2-seitige
Signifikanz von 0.348 ist weit größer als das erforderliche Kriterium
0.05 .