Dr.Quapp: Statistik für Mathematiker mit SPSS
8. Übung - Faltung + Grenzwertsatz
- 1.
- Erzeugen Sie (je 200 Zeilen) von zwei diskreten
Zufallsgrößen
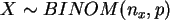 , und
, und
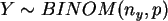 und bilden Sie damit die neuen Zufallsgröße
und bilden Sie damit die neuen Zufallsgröße
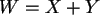 .
Überprüfen Sie das bekannte Faltungsverhalten der Binomialverteilung,
d.h. berechnen Sie die resultierenden Parameter
.
Überprüfen Sie das bekannte Faltungsverhalten der Binomialverteilung,
d.h. berechnen Sie die resultierenden Parameter 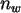 und
und 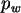 .
.
- 2.
- Erzeugen Sie (je 200 Zeilen) von zwei diskreten
Zufallsgrößen
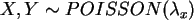 ,
,
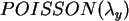 und bilden Sie damit
die neuen Zufallsgrößen
und bilden Sie damit
die neuen Zufallsgrößen
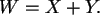 Überprüfen Sie das bekannte Faltungsverhalten der Poissonverteilung,
d.h. berechnen Sie den resultierenden Parameter
Überprüfen Sie das bekannte Faltungsverhalten der Poissonverteilung,
d.h. berechnen Sie den resultierenden Parameter 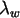 für ein
für ein
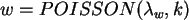 .
.
- 3.
- Erzeugen Sie (je 200 Zeilen) von zwei
Zufallsgrößen
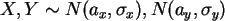 und bilden Sie damit neue Zufallsgrößen
und bilden Sie damit neue Zufallsgrößen
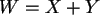 und
und 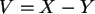 .
Überprüfen Sie das bekannte Faltungsverhalten der Normalverteilung,
d.h. berechnen Sie die resultierenden Mittelwerte und Streuungen von
.
Überprüfen Sie das bekannte Faltungsverhalten der Normalverteilung,
d.h. berechnen Sie die resultierenden Mittelwerte und Streuungen von  und
und
 .
.
- 4.
- Erzeugen Sie (je 200 Zeilen) von zwei
Zufallsgrößen
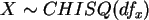 , und
, und
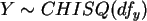 und bilden Sie damit
die neuen Zufallsgrößen
und bilden Sie damit
die neuen Zufallsgrößen
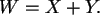 Überprüfen Sie das bekannte Faltungsverhalten der
Überprüfen Sie das bekannte Faltungsverhalten der 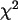 -Verteilung,
d.h. berechnen Sie den resultierenden Parameter
-Verteilung,
d.h. berechnen Sie den resultierenden Parameter 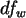 .
.
l
- 5.
- Die Binomialverteilung
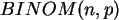 läßt sich durch die Normalverteilung
approximieren,
wenn
läßt sich durch die Normalverteilung
approximieren,
wenn 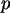 nicht zu nahe an 0 oder 1 ist, und
wenn
nicht zu nahe an 0 oder 1 ist, und
wenn 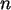 hinreichend groß ist (zentraler Grenzwertsatz).
Vergleichen Sie mit
hinreichend groß ist (zentraler Grenzwertsatz).
Vergleichen Sie mit 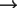 Streu-Diagramm die
Verteilungsfunktionen von N(0,1) und der
entsprechend verschobenen Verteilungsfunktion der Binomialverteilung
für
Streu-Diagramm die
Verteilungsfunktionen von N(0,1) und der
entsprechend verschobenen Verteilungsfunktion der Binomialverteilung
für 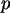 =1/3 und
=1/3 und 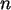 =10, 30, 100, und 300.
=10, 30, 100, und 300.
Hinweis: "verschoben" verwendet,
wenn
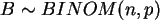 ist, dann sollte
ist, dann sollte
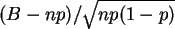 näherungsweise nach
näherungsweise nach 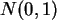 verteilt sein.
In SPSS kann damit die Binomialverteilung auf einer ganzzahligen
Achsenvariablen
verteilt sein.
In SPSS kann damit die Binomialverteilung auf einer ganzzahligen
Achsenvariablen 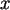 ( mit
( mit 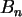 =CDF.BINOM(x,n,1/3) ) verschoben werden zu
der neuen Achsenvariablen
=CDF.BINOM(x,n,1/3) ) verschoben werden zu
der neuen Achsenvariablen 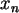 durch
durch
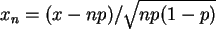 . Mit dieser
sind je zwei Verteilungen
. Mit dieser
sind je zwei Verteilungen 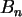 und
und 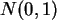 gleichzeitig betrachtbar.
Die 4 Fälle für
gleichzeitig betrachtbar.
Die 4 Fälle für 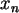 sind einzeln zu behandeln.
sind einzeln zu behandeln.
Führen Sie zu allen Aufgaben auch die entsprechenden theoretischen
Rechnungen durch!
Dr.Wolfgang Quapp
2004-11-30