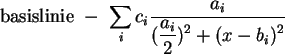Dr.Quapp: Statistik für Mathematiker mit SPSS
4. Übung - Nichtlineare Regression und
Partielle Korrelation
- 1.
- a) Es seien
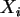
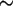 N(0,1) und
N(0,1) und 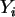
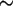 N(0,1)
unabhängige
Zufallsgrößen. Wir bilden
N(0,1)
unabhängige
Zufallsgrößen. Wir bilden
Zeigen Sie, daß Cov(V,W)= a a + b b
+ b b ist.
ist.
b) Erzeugen Sie 1000 Zufallszahlen von V und W. Wählen Sie dabei a,
a , b, b
, b, b so, daß gilt
so, daß gilt
- 2.
- Laden Sie die Datei HCN1.sav von D:
Die Werte sind experimentelle Resultate eines Spektrometers, mit welchem
Vibrations-Rotationslinien des HCN-Moleküles gemessen wurden.
Es wird aus theoretischen Betrachtungen geschlossen, daß einzelne
Linien additiv überlagern, und die Bandenform mit der sogenannten
Lorenz-Funktion beschrieben werden kann:
Der Laufindex 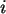 gibt die Nummer der Linie an, und
a,b,c sind für jede Linie zu findende Parameter:
gibt die Nummer der Linie an, und
a,b,c sind für jede Linie zu findende Parameter:
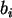 sind die Lageparameter,
sind die Lageparameter, 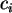 geben die
Größe = Intensität der Linien an, und
geben die
Größe = Intensität der Linien an, und 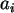 beschreiben die sogenannte Halbwertbreite.
beschreiben die sogenannte Halbwertbreite.
 sei die Achsenvariable.
sei die Achsenvariable.
- 3.
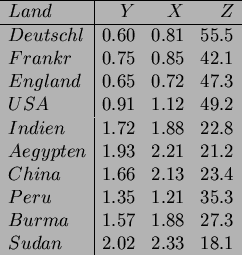
- Es wird ein Zusammenhang vermutet zwischen der Zahl der Geburten
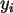 eines Landes (je 100 Einwohner) und der Zahl der Störche
eines Landes (je 100 Einwohner) und der Zahl der Störche 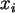 (pro 100 km
(pro 100 km ) ??? Der Zusammenhang läßt sich aber stark
"auspartialisieren", wenn man den Industrialisierungsgrad
) ??? Der Zusammenhang läßt sich aber stark
"auspartialisieren", wenn man den Industrialisierungsgrad 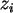 mit
beachtet (Anteil der Industrieproduktion am Sozialprodukt)
Datei stoerche.sav von D:
mit
beachtet (Anteil der Industrieproduktion am Sozialprodukt)
Datei stoerche.sav von D:
Bestimmen Sie die bivariaten und die partiellen Korrelationen und deuten Sie
diese.
- 4.
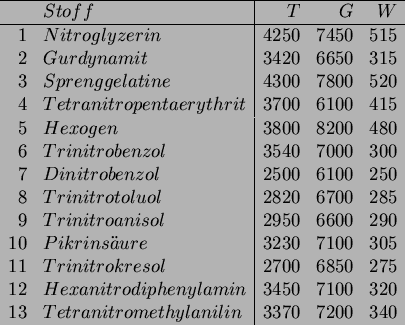
- Laden Sie die Datei explo.sav von D:
Die Werte geben die Wirkung W (in cm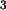 ) von verschiedenen Sprengstoffen an,
wobei vermutet wird, daß diese abhängt von der Explosionstemperatur
T (in
) von verschiedenen Sprengstoffen an,
wobei vermutet wird, daß diese abhängt von der Explosionstemperatur
T (in  C), und von der Detonationsgeschwindigkeit G (in m/sec).
C), und von der Detonationsgeschwindigkeit G (in m/sec).
a) Bestimmen Sie durch lineare Regression die beste
Funktion der Art
b) Bestimmen Sie die bivariaten und die partiellen Korrelationen und deuten Sie
diese.
Dr.Wolfgang Quapp
2004-10-26