2.)
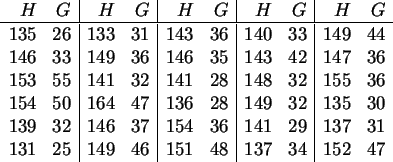
Die folgende Tabelle enthält die Größe (![]() in cm) und das
Gewicht (
in cm) und das
Gewicht (![]() in kg) von
in kg) von ![]() elfjährigen Mädchen
(datei hoehe30.sav in D: ).
elfjährigen Mädchen
(datei hoehe30.sav in D: ).
Die Werte können von SPSS-Nutzern geladen werden;
danach gehe man wieder auf sein
home-directory, um beim Abspeichern nicht die vorhandene Datei zu
beschädigen.
zu a) und b) und c) Wie gehabt gehe man zu Analysieren,
deskriptive Statistik, und klicke die
entsprechenden Felder an.
Bei c) ist direkt zu berechnen die mittleren absoluten Abweichung:
| 1 | 2 | 3 | |
| 1 | 10 | 2 | 0 |
| 2 | 2 | 5 | 4 |
| 3 | 0 | 2 | 5 |
3.) Erzeugen Sie je 100 normalverteilte Zufallszahlen
![]()
![]() N(0,1) und
N(0,1) und ![]()
![]() N(0,0.5)
N(0,0.5)
(verwenden Sie den Befehl RV.Normal(...) im Fenster Berechnen).
a) Stellen Sie die Dichten von ![]() und
und ![]() grafisch dar.
grafisch dar.
Erzeugen Sie je 100 weitere Zufallszahlen mittels
![]()
![]() 10
10![]()
![]() + 3 + 0.1
+ 3 + 0.1![]() ,
,
![]()
![]() 10
10![]()
![]() + 3 + 0.5
+ 3 + 0.5![]() sowie
sowie
![]()
![]() 10
10![]()
![]() + 3 + 2.0
+ 3 + 2.0![]() .
.
(Hinweis: schräg zu den Zeilen kann man Variable mit den Befehlen
Leads und Lag verwenden.)
b) Bestimmen Sie die Korrelationen zwischen den neuen Variablen
und ![]() .
.
c) Bestimmen Sie die beste lineare und die beste quadratische Anpassung
von ![]() ,
, ![]() und
und ![]() zu
zu ![]() . Wie sinnvoll ist letzteres?
. Wie sinnvoll ist letzteres?
Zuerst muß dem System von SPSS mitgeteilt werden, daß 100 "Fälle"
zu behandeln sind: Durch Anklicken eines Feldes in der 100sten Zeile des
Datenfeldes und Belegen mit einem Wert.
Im Fenster Transformieren, Berechnen kann der Befehl RV.Random geladen werden.
zu a) Das Resultat sind 100 zufällig verteilte Werte, die sich ungeordnet
auf einer Zahlen-Achse befinden. Man kann diese sofort als Dichte
veranschaulichen durch Aufruf des Histogramms für X oder U,
welches automatisch eine
Klasseneinteilung, und die Sortierung in die Klassen vornimmt.
(Es zeigt sich, daß bei 100 noch keine allzu perfekte
"Zufälligkeit" erreicht ist!)
Bei der Berechnung von Y und W ist zu beachten, daß Werte
schräg zu den Zeilen verknüpft werden sollen: Zeile i mit i+1 oder i-1.
Bei W soll zurückgegriffen werden, dazu dient LAG, welches im
Fenster Transformieren, Berechnen vorhanden ist:
W=10![]() X+3+2
X+3+2![]() LAG(U) .
Bei Y soll vorausgegriffen werden. Dies leistet LEAD, das allerdings extra
aufgerufen werden muß: Es ist im Fenster Transformieren, Zeitreihen
versteckt; (analog zur kumulativen Summe).
LAG(U) .
Bei Y soll vorausgegriffen werden. Dies leistet LEAD, das allerdings extra
aufgerufen werden muß: Es ist im Fenster Transformieren, Zeitreihen
versteckt; (analog zur kumulativen Summe).
zu c) Man rufe auf Regression, Kurvenanpassung, und klicke dort noch
den quadratischen Fall an. Es zeigt sich , daß die quadratische Regression
"vernünftig" arbeitet: Da in diesem Fall eine ziemlich klare lineare
Abhängigkeit vorliegt, sind die berechneten Koeffizienten des quadratischen
Gliedes faktisch Null.
Bei dem vorgeschlagenem Fenster wird auch eine Grafik der Lösung mit
ausgegeben.
4.)
Gegeben sei folgende Tabelle:
Die kleine Tabelle ist so konstruiert, daß die Werte der Variablen auch
gleichzeitig ihre Platz-Ziffern=Ränge sind.
In Statistik, Korrelation, Bivariat klicke man entsprechende Felder an.
Es resultiert dann