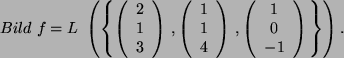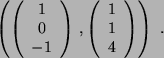
Für

(ii) Der Kern besteht aus allen Vektoren, die auf
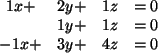
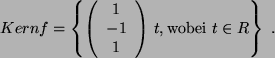 Es ist
Es ist
Das Bild von ![]() ist die lineare Hülle der Abbildungen der
Basisvektoren des Urbildraumes:
ist die lineare Hülle der Abbildungen der
Basisvektoren des Urbildraumes:
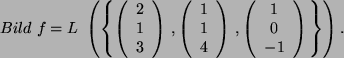
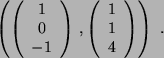
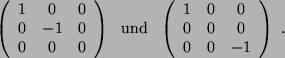


Für

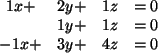
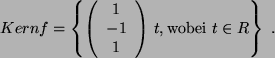 Es ist
Es ist
Das Bild von ![]() ist die lineare Hülle der Abbildungen der
Basisvektoren des Urbildraumes:
ist die lineare Hülle der Abbildungen der
Basisvektoren des Urbildraumes: