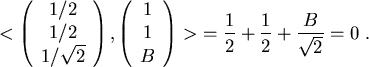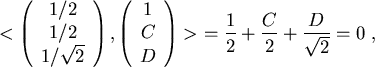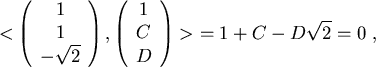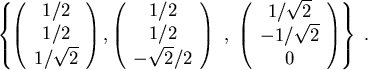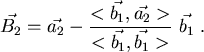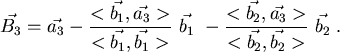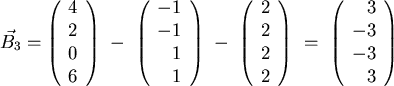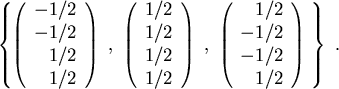Dr.Quapp HS 2002
http://www.mathe.uni-leipzig.de/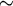 quapp/uebungenP.html
quapp/uebungenP.html
Lösungen zur 12. Übung (zum 20. 1. 2003)
- 50.
- Die Cauchy-Schwarzsche Ungleichung lautet
Der Winkel zwischen den beiden Vektoren ist
Wenn in der Relation das Gleichheitszeichen steht, dann ist
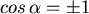 , also
, also 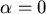 oder
oder 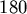 Grad. Dann sind
Grad. Dann sind 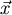 und
und
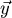 linear abhängig.
linear abhängig.
- 51.
- Der Vektor
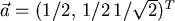 ist zu einer
Orthonormalbasis zu ergänzen.
ist zu einer
Orthonormalbasis zu ergänzen.
(i) Setze an mit einem Vektor 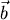
Es folgt 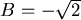 , und der Betrag des neuen Vektors ist
, und der Betrag des neuen Vektors ist
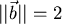 .
.
(ii) Suche nun einen Vektor 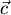 , der zu den beiden gegebenen
orthogonal ist
, der zu den beiden gegebenen
orthogonal ist
also
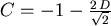 , und
, und
also ergibt sich als zweite Gleichung
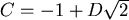 ; daraus
; daraus
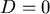 und
und 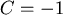 .
Der Betrag des 3. Vektors ist
.
Der Betrag des 3. Vektors ist
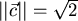 .
Eine Orthonormalbasis ist:
.
Eine Orthonormalbasis ist:
- 52.
- Gegeben sind 3 Vektoren im
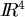 :
:
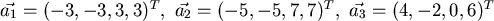 .
Der erste wird normiert zu
.
Der erste wird normiert zu
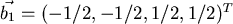 .
Dann ist ein orthogonaler Vektor
.
Dann ist ein orthogonaler Vektor
Das Skalarprodukt im Zähler ist 12, im Nenner wegen der vorherigen
Normierung 1. Damit ist
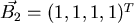 , und nach erneuter Normierung
erhalten wir
, und nach erneuter Normierung
erhalten wir
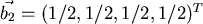 .
Nun kann der 3.Vektor berechnet werden:
.
Nun kann der 3.Vektor berechnet werden:
Die Skalarprodukte in den beiden Zählern sind 2 und 4.
Somit wird
Der Betrag des 3. Vektors ist
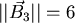 ,
und nach erneuter Normierung
erhalten wir
,
und nach erneuter Normierung
erhalten wir
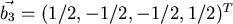 .
Die ONB ist letztendlich:
.
Die ONB ist letztendlich:
- 53.
- Es sei definiert ein Skalarprodukt
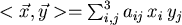 , wobei die
Koeffizienten
, wobei die
Koeffizienten 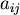 in folgender Matrix festgelegt sind:
in folgender Matrix festgelegt sind:
Damit ist
Analog ergibt sich
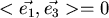 und
und
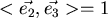 .
Die Beträge sind auch nach diesem Schema zu berechnen, es ist:
.
Die Beträge sind auch nach diesem Schema zu berechnen, es ist:
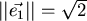 ,
,
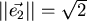 , und
, und
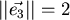 .
.
Die Winkel werden:
Dr.Wolfgang Quapp
2003-02-06
![]() quapp/uebungenP.html
quapp/uebungenP.html