Dr.Quapp
HS 2002
http://www.mathe.uni-leipzig.de/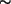 quapp/uebungenP.html
quapp/uebungenP.html
Lineare Algebra - Lösungen zur 10. Übung (zum 6. 1. 2003)
- 42.
- Eine Permutationsmatrix entsteht aus der Einheitsmatrix, indem man
z.b.
 -mal eine Zeilenvertauschung vornimmt.
Umgekehrt kann man jede Permutationsmatrix in die Einheitsmatrix
überführen, indem man diese entsprechenden
-mal eine Zeilenvertauschung vornimmt.
Umgekehrt kann man jede Permutationsmatrix in die Einheitsmatrix
überführen, indem man diese entsprechenden  Zeilenvertauschungen
invers vornimmt. Bei jeder Zeilenvertauschung ändert sich das
Vorzeichen der Determinante um
Zeilenvertauschungen
invers vornimmt. Bei jeder Zeilenvertauschung ändert sich das
Vorzeichen der Determinante um 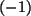 , also bei
, also bei  Zeilenvertauschungen um
Zeilenvertauschungen um 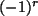 .
Die gesuchte Determinante ist
.
Die gesuchte Determinante ist 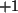 oder
oder 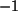 .
.
- 43.
- Die Lösung durch eine Zeilenstufen-Berechnung ist bei Aufgabe (a)
- 44.
- Wäre
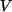 ein VR mit 3 Elementen, so ist es naheliegend anzunehmen,
dass diese
ein VR mit 3 Elementen, so ist es naheliegend anzunehmen,
dass diese
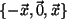 sind, weil
sind, weil 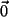 ein
Element sein muss, und zu
ein
Element sein muss, und zu 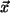 soll es das entgegengesetzte
Element
soll es das entgegengesetzte
Element 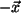 geben. Sei wie immer
geben. Sei wie immer
 oder
oder 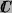 ,
und
,
und
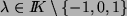 , dann ergibt sich bei den Rechenregeln für
, dann ergibt sich bei den Rechenregeln für
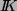 sofort, dass
sofort, dass
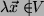 . Somit kann es keinen VR
über
. Somit kann es keinen VR
über 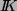 mit 3 Elementen geben.
mit 3 Elementen geben.
- 45.
- Sei
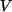 der VR der (2,2) Matrizen mit reellen Einträgen.
der VR der (2,2) Matrizen mit reellen Einträgen.
(a)
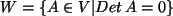 .
.
Wäre  ein VR, so müsste die Addition seiner Elemente in
ein VR, so müsste die Addition seiner Elemente in  bleiben. Ein Gegenbeispiel bringt diese Annahme zu Fall:
Wähle
Es ist offenbar
bleiben. Ein Gegenbeispiel bringt diese Annahme zu Fall:
Wähle
Es ist offenbar
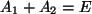 , und obwohl die
, und obwohl die 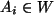 sind, ist
sind, ist
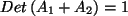 .
.
Also ist  kein Untervektorraum von
kein Untervektorraum von 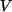 .
.
(b)
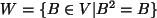 .
.
Wäre  ein VR, so müsste wieder die Addition seiner Elemente in
ein VR, so müsste wieder die Addition seiner Elemente in  bleiben. Ein Gegenbeispiel bringt auch diese Annahme zu Fall:
Wähle
bleiben. Ein Gegenbeispiel bringt auch diese Annahme zu Fall:
Wähle
Es ist aber offenbar
 .
.
Also ist  kein Untervektorraum von
kein Untervektorraum von 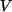 .
.
Bemerkung: Matrizen dieser Menge  mit
mit 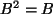 sind sogenannte
Projektoren.
sind sogenannte
Projektoren.
- 45.c)
- Wir haben zu betrachten:
Das sind 4 Gleichungen eines homogenen Systems für die 3
Koeffizienten. Aus der 3.Gleichung (für die untere linke
Komponente) ergibt sich direkt  , dann aus der
4.Gleichung (für die untere rechte Komponente)
, dann aus der
4.Gleichung (für die untere rechte Komponente) 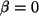 , und
somit auch noch
, und
somit auch noch 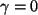 . Also sind die 3 Elemente linear unabhängig.
. Also sind die 3 Elemente linear unabhängig.
Dr.Wolfgang Quapp
2003-01-27
![]() quapp/uebungenP.html
quapp/uebungenP.html
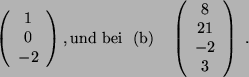
![]() .
.
![]() ein VR, so müsste wieder die Addition seiner Elemente in
ein VR, so müsste wieder die Addition seiner Elemente in ![]() bleiben. Ein Gegenbeispiel bringt auch diese Annahme zu Fall:
Wähle
bleiben. Ein Gegenbeispiel bringt auch diese Annahme zu Fall:
Wähle
![]() , dann aus der
4.Gleichung (für die untere rechte Komponente)
, dann aus der
4.Gleichung (für die untere rechte Komponente) ![]() , und
somit auch noch
, und
somit auch noch ![]() . Also sind die 3 Elemente linear unabhängig.
. Also sind die 3 Elemente linear unabhängig.