Dr.Quapp: Statistik für Mathematiker mit SPSS
Hinweise zur 10. Übung - Stichproben -
1.] a) Ein Massenartikel ( N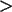 15000 ) habe eine
NORMAL-verteilte Ausschußrate von p=10% (Nullhypothese).
15000 ) habe eine
NORMAL-verteilte Ausschußrate von p=10% (Nullhypothese).
Eine Stichprobe von n=100 soll diese Nullhypothese überprüfen.
Berechnen Sie zum Signifikationsniveau 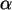 =0,05 den kritischen
Wert der Testgröße für n.
=0,05 den kritischen
Wert der Testgröße für n.
Anleitung: Im Intervall von 0 bis 0,3 für p für etwa p(i) mit
i=1,...,300 Werte
die Dichte der Normalverteilung direkt berechnen; und diese bis zum
kritischen Wert 0,95 aufsummieren.
Für die Varianz gilt näherungsweise 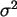 =p
=p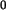 (1-p
(1-p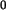 ) /n,
da erfüllt ist: n/N
) /n,
da erfüllt ist: n/N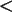 0,05.
0,05.
Skalieren Sie noch probeweise den p-Bereich auf
Standardwerte z.
b) Die Alternativ-Hypothese der Ausschußrate sei p=20% .
Die Stichprobe von n=100 soll auch diese Hypothese überprüfen.
Berechnen Sie zu (a) den entsprechenden 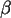 -Fehler.
-Fehler.
Anleitung: Im Intervall von 0 bis 0,3 für p für etwa p(i) mit
i=1,..., 300 Werte
die Dichte der Normalverteilung mit p=0,2 direkt berechnen; und bis zum
kritischen Wert von Aufgabe (a) aufsummieren.
Für die Varianz gilt
nun näherungsweise 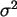 =p
=p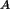 (1-p
(1-p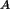 ) /n.
) /n.
c) Zeichnen Sie mit Hilfe von STREUPLOT die empirischen
Dichten für p=0,1 und p=0,2 übereinander. Welches sind die Gebiete der
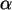 - und
- und 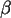 -Fehler? Mit SequencePlot sind diese schraffierbar.
-Fehler? Mit SequencePlot sind diese schraffierbar.
2] Ein Massenartikel ( N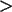 15000 ) sei normalverteilt: Wir
betrachten die Mast von Hähnchen.
Der Mittelwert des Gewichtes sei
15000 ) sei normalverteilt: Wir
betrachten die Mast von Hähnchen.
Der Mittelwert des Gewichtes sei 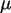 =492,5g bei einer
Standardabweichung von
=492,5g bei einer
Standardabweichung von 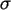 =18,9g.
=18,9g.
Mit einer Stichprobe von n=81
Tieren ergibt ein Fütterungsversuch mit einem anderen Futter das
Resultat der Datei MASTHAHN.SAV.
Man kann annehmen, daß die Standardabweichung dabei nicht vom Futter
abhängt. Kann man auf Grund des Stichproben-Versuches schließen, daß
das neue Futter zu besseren Resultaten der Mast führt?
Die Antwort soll zu einem Signifikanzniveau 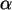 =0.01 erfolgen.
=0.01 erfolgen.
3] Es wurden 10 Stichproben eines Glyzerin-Wasser-Gemisches
gezogen. Es ergaben sich folgende Dichten (in g/cm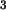 ):
):
1,0768,
1,0772,
1,0766,
1,0765,
1,0774,
1,0771,
1,0775,
1,0770,
1,0769,
1,0770.
Es ist zu prüfen, ob das Gemisch aus 30% Glyzerin besteht, für das
die mittlere Dichete mit 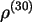 =1,0771 angegeben wird.
=1,0771 angegeben wird.
Dr.Wolfgang Quapp
2004-11-30