Dr.Quapp: Statistik für Mathematiker mit SPSS

3. Übung - Regression

1.

Es wird ein Zusammenhang vermutet zwischen dem Schwefelgehalt $s_i$ der Luft (in $\mu g/m^3$) und den Absenzen $z_i$ von weiblichen Angestellten (pro 1000 Angestellte) in 5 Städten:

$$\begin{array}{r\vert rrrrr} \hline s_i & 7& 13 & 14 & 17 & 20 \\ \hline z_i & 19& 44 & 53 & 61 & 88 \\ \hline \end{array}$$

Bestimmen Sie durch lineare Regression die beste Funktion $z = a + b s$ sowie auch die beste Funktion $s = A + B z$, und vergleichen Sie beide Resultate durch Darstellung in einem Koordinatensystem: Schnittpunkt, Winkel zwischen den Geraden?

2.

Die folgende Tabelle enthält die Größe ($H$ in cm) und das Gewicht ($G$ in kg) von $30$ elfjährigen Mädchen (datei hoehe30.sav in D: ).

$$\begin{array}{rr\vert rr\vert rr\vert rr\vert rr} H&G&H&G&H&... ... 131& 25& 149& 46 & 151& 48& 137& 34 & 152 & 47\\ \end{array}$$

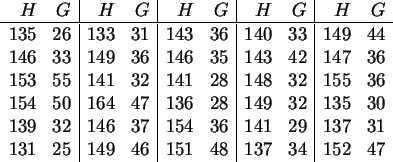
Untersuchen Sie zunächst die Merkmale $G$ und $H$ separat.
a) Bestimmen Sie für $G$ und $H$ die Häufigkeitstabellen und Histogramme.
b) Bestimmen Sie für beide Merkmale Modalwert, Median, arithmetisches Mittel und die Quartile der Ordnung 1/4 bzw. 3/4.
c) Bestimmen Sie die Standardabweichungen, Schiefen, Wölbungen beider Merkmale und die mittleren absoluten Abweichungen.
Untersuchen Sie die Abhängigkeit der Merkmale $G$ und $H$.
d) Zeichnen Sie das Streuungsdiagramm.
e) Bestimmen Sie durch lineare Regression die beste Funktion $G = a + b H$.
f) Klassifizieren Sie $G$ und $H$ in je 3 Klassen und Stellen Sie die Kontingenztafel auf.

3.

Erzeugen Sie je 100 normalverteilte Zufallszahlen $X_i$$\sim$N(0,1) und $U_i$$\sim$N(0,0.5)
(verwenden Sie den Befehl RV.Normal(...) im Fenster Berechnen).
a) Stellen Sie die Dichten von $X$ und $U$ grafisch dar.
Erzeugen Sie je 100 weitere Zufallszahlen mittels
$Y_i$$\sim$ 10$*$$X_i$ + 3 + 0.1$*U_{(i+1)}$,
$Z_i$$\sim$ 10$*$$X_i$ + 3 + 0.5$*U_i$ sowie
$W_i$$\sim$ 10$*$$X_i$ + 3 + 2.0$*U_{(i-1)}$ .
(Hinweis: schräg zu den Zeilen kann man Variable mit den Befehlen Leads und Lag verwenden.)
b) Bestimmen Sie die Korrelationen zwischen den neuen Variablen und $X_i$.
c) Bestimmen Sie die beste lineare und die beste quadratische Anpassung von $Y_i$, $Z_i$ und $W_i$ zu $X_i$ . Wie sinnvoll ist letzteres?

4.

Gegeben sei folgende Tabelle:

$$\begin{array}{r\vert rrrrrrrrrr} \hline x&2&2&2&7&7&7&7&7&7&7\\ \hline y&1&3&3&3&6&6&6&9&9&9 \\ \hline \end{array}$$

a) Bestimmen Sie den Pearsonschen und den Spearmanschen Korrelationskoeffizienten.
b) Bestimmen Sie durch lineare Regression die beste Funktion $y = a + b\, x$.
c) Geben Sie eine Kreuztabelle an.